Question-91399

Question Number 91399 by jagoll last updated on 30/Apr/20

Commented by Prithwish Sen 1 last updated on 30/Apr/20

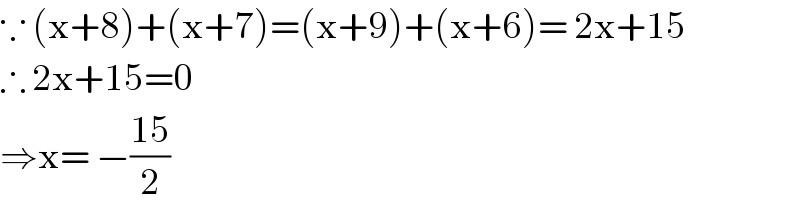
∵ (x+8)+(x+7)=(x+9)+(x+6)= 2x+15 ∴ 2x+15=0 ⇒x= −((15)/2)

$$\because\:\left(\mathrm{x}+\mathrm{8}\right)+\left(\mathrm{x}+\mathrm{7}\right)=\left(\mathrm{x}+\mathrm{9}\right)+\left(\mathrm{x}+\mathrm{6}\right)=\:\mathrm{2x}+\mathrm{15} \\ $$$$\therefore\:\mathrm{2x}+\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\:−\frac{\mathrm{15}}{\mathrm{2}} \\ $$

Commented by jagoll last updated on 30/Apr/20

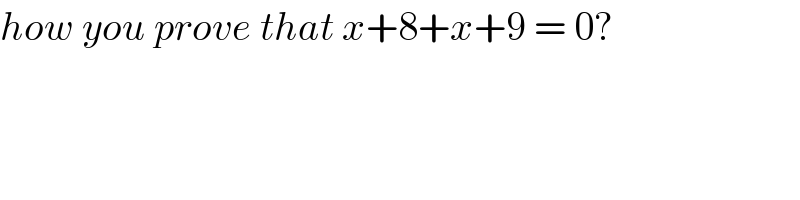
$${how}\:{you}\:{prove}\:{that}\:{x}+\mathrm{8}+{x}+\mathrm{9}\:=\:\mathrm{0}? \\ $$

Commented by $@ty@m123 last updated on 30/Apr/20

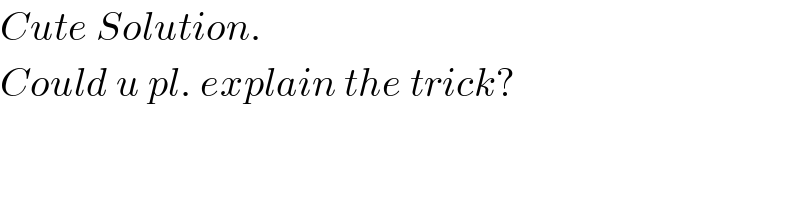
$${Cute}\:{Solution}. \\ $$$${Could}\:{u}\:{pl}.\:{explain}\:{the}\:{trick}? \\ $$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

$$\mathrm{it}\:\mathrm{is}\:\mathrm{vedic}\:\:\mathrm{maths}.\: \\ $$

Commented by jagoll last updated on 30/Apr/20

$${vedic}\:{math}? \\ $$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

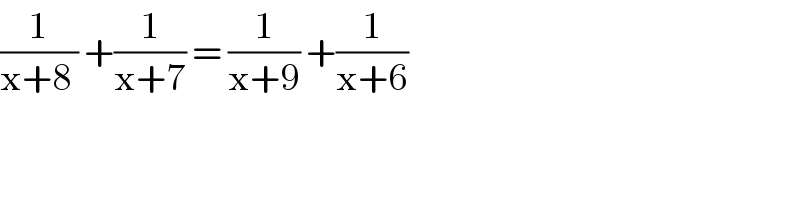
(1/(x+8 )) +(1/(x+7)) = (1/(x+9)) +(1/(x+6))

$$\frac{\mathrm{1}}{\mathrm{x}+\mathrm{8}\:}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{7}}\:=\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{9}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{6}} \\ $$

Commented by jagoll last updated on 30/Apr/20

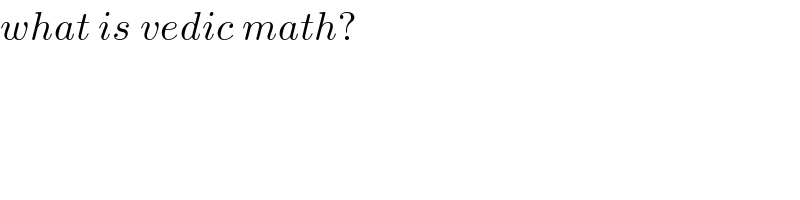
$${what}\:{is}\:{vedic}\:{math}? \\ $$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

(2x+15)[(1/((x+8)(x+7))) −(1/((x+9)(x+6)))]=0 ∵ 8+7 = 9+6 and the term x^2 vanishes then 2x+15 = 0

$$\left(\mathrm{2x}+\mathrm{15}\right)\left[\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{8}\right)\left(\mathrm{x}+\mathrm{7}\right)}\:−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{9}\right)\left(\mathrm{x}+\mathrm{6}\right)}\right]=\mathrm{0} \\ $$$$\because\:\mathrm{8}+\mathrm{7}\:=\:\mathrm{9}+\mathrm{6}\:\:\mathrm{and}\:\mathrm{the}\:\mathrm{term}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{vanishes} \\ $$$$\mathrm{then}\:\mathrm{2x}+\mathrm{15}\:=\:\mathrm{0} \\ $$

Commented by jagoll last updated on 30/Apr/20

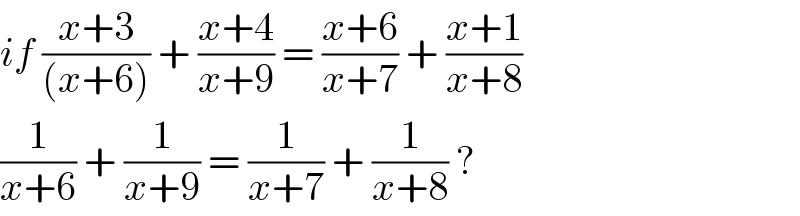
if ((x+3)/((x+6))) + ((x+4)/(x+9)) = ((x+6)/(x+7)) + ((x+1)/(x+8)) (1/(x+6)) + (1/(x+9)) = (1/(x+7)) + (1/(x+8)) ?

$${if}\:\frac{{x}+\mathrm{3}}{\left({x}+\mathrm{6}\right)}\:+\:\frac{{x}+\mathrm{4}}{{x}+\mathrm{9}}\:=\:\frac{{x}+\mathrm{6}}{{x}+\mathrm{7}}\:+\:\frac{{x}+\mathrm{1}}{{x}+\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{{x}+\mathrm{6}}\:+\:\frac{\mathrm{1}}{{x}+\mathrm{9}}\:=\:\frac{\mathrm{1}}{{x}+\mathrm{7}}\:+\:\frac{\mathrm{1}}{{x}+\mathrm{8}}\:?\: \\ $$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

Commented by Prithwish Sen 1 last updated on 30/Apr/20

Commented by jagoll last updated on 30/Apr/20

$${waw}..{great}…\:{thank}\:{you} \\ $$

Commented by $@ty@m123 last updated on 30/Apr/20

$${Thanks} \\ $$

Answered by jagoll last updated on 30/Apr/20

Answered by Rasheed.Sindhi last updated on 30/Apr/20

((x+7)/(x+8))−1+((x+6)/(x+7))−1=((x+8)/(x+9))−1+((x+5)/(x+6))−1 ((−1)/(x+8))+((−1)/(x+7))=((−1)/(x+9))+((−1)/(x+6)) (1/(x+8))+(1/(x+7))=(1/(x+9))+(1/(x+6)) ((2x+15)/((x+8)(x+7)))−((2x+15)/((x+9)(x+6)))=0 (2x+15){(1/((x+8)(x+7)))−(1/((x+9)(x+6)))}=0 •2x+15=0⇒x=−15/2 •(x^2 +15x+54)−(x^2 +15x+56)=0 ⇒ No root

$$\frac{{x}+\mathrm{7}}{{x}+\mathrm{8}}−\mathrm{1}+\frac{{x}+\mathrm{6}}{{x}+\mathrm{7}}−\mathrm{1}=\frac{{x}+\mathrm{8}}{{x}+\mathrm{9}}−\mathrm{1}+\frac{{x}+\mathrm{5}}{{x}+\mathrm{6}}−\mathrm{1} \\ $$$$\frac{−\mathrm{1}}{{x}+\mathrm{8}}+\frac{−\mathrm{1}}{{x}+\mathrm{7}}=\frac{−\mathrm{1}}{{x}+\mathrm{9}}+\frac{−\mathrm{1}}{{x}+\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{{x}+\mathrm{8}}+\frac{\mathrm{1}}{{x}+\mathrm{7}}=\frac{\mathrm{1}}{{x}+\mathrm{9}}+\frac{\mathrm{1}}{{x}+\mathrm{6}} \\ $$$$\frac{\mathrm{2}{x}+\mathrm{15}}{\left({x}+\mathrm{8}\right)\left({x}+\mathrm{7}\right)}−\frac{\mathrm{2}{x}+\mathrm{15}}{\left({x}+\mathrm{9}\right)\left({x}+\mathrm{6}\right)}=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}+\mathrm{15}\right)\left\{\frac{\mathrm{1}}{\left({x}+\mathrm{8}\right)\left({x}+\mathrm{7}\right)}−\frac{\mathrm{1}}{\left({x}+\mathrm{9}\right)\left({x}+\mathrm{6}\right)}\right\}=\mathrm{0} \\ $$$$\bullet\mathrm{2}{x}+\mathrm{15}=\mathrm{0}\Rightarrow{x}=−\mathrm{15}/\mathrm{2} \\ $$$$\bullet\left({x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{54}\right)−\left({x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{56}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{No}\:{root} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply