Question Number 91465 by Zainal Arifin last updated on 30/Apr/20

Commented by Prithwish Sen 1 last updated on 01/May/20
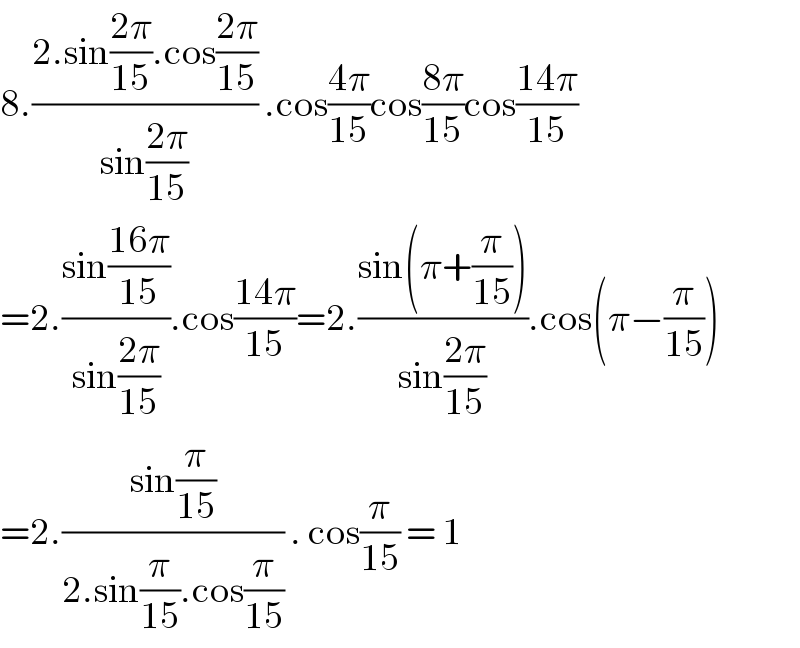
$$\mathrm{8}.\frac{\mathrm{2}.\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{15}}.\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{15}}}{\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{15}}}\:.\mathrm{cos}\frac{\mathrm{4}\pi}{\mathrm{15}}\mathrm{cos}\frac{\mathrm{8}\pi}{\mathrm{15}}\mathrm{cos}\frac{\mathrm{14}\pi}{\mathrm{15}} \\ $$$$=\mathrm{2}.\frac{\mathrm{sin}\frac{\mathrm{16}\pi}{\mathrm{15}}}{\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{15}}}.\mathrm{cos}\frac{\mathrm{14}\pi}{\mathrm{15}}=\mathrm{2}.\frac{\mathrm{sin}\left(\pi+\frac{\pi}{\mathrm{15}}\right)}{\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{15}}}.\mathrm{cos}\left(\pi−\frac{\pi}{\mathrm{15}}\right) \\ $$$$=\mathrm{2}.\frac{\mathrm{sin}\frac{\pi}{\mathrm{15}}}{\mathrm{2}.\mathrm{sin}\frac{\pi}{\mathrm{15}}.\mathrm{cos}\frac{\pi}{\mathrm{15}}}\:.\:\mathrm{cos}\frac{\pi}{\mathrm{15}}\:=\:\mathrm{1}\: \\ $$
Answered by john santu last updated on 01/May/20

$${let}\:\frac{\pi}{\mathrm{15}}\:=\:{w}\:,\:\mathrm{cos}\:\frac{\mathrm{14}\pi}{\mathrm{15}}\:=\:\mathrm{cos}\left(\pi−\frac{\pi}{\mathrm{15}}\right)\: \\ $$$$=\:−\mathrm{cos}\:\frac{\pi}{\mathrm{15}} \\ $$$$\Rightarrow\:\frac{−\mathrm{16cos}\:{w}\:\mathrm{cos}\:\mathrm{2}{w}\:\mathrm{cos}\:\mathrm{4}{w}\:\mathrm{cos}\:\mathrm{8}{w}}{\mathrm{sin}\:{w}}\:×\:\mathrm{sin}\:{w}\:= \\ $$$$\frac{−\mathrm{8}\:\mathrm{sin}\:\mathrm{2}{w}\:\mathrm{cos}\:\mathrm{2}{w}\:\mathrm{cos}\:\mathrm{4}{w}\:\mathrm{cos}\:\mathrm{8}{w}}{\mathrm{sin}\:{w}}\:= \\ $$$$\frac{−\mathrm{4sin}\:\mathrm{4}{w}\:\mathrm{cos}\:\mathrm{4}{w}\:\mathrm{cos}\:\mathrm{8}{w}}{\mathrm{sin}\:{w}}\:= \\ $$$$\frac{−\mathrm{2sin}\:\mathrm{8}{w}\:\mathrm{cos}\:\mathrm{8}{w}}{\mathrm{sin}\:{w}}\:=\:\frac{−\mathrm{sin}\:\mathrm{16}{w}}{\mathrm{sin}\:{w}} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{16}\pi}{\mathrm{15}}\right)\:=\:\mathrm{sin}\:\left(\pi+\frac{\pi}{\mathrm{15}}\right)\:=\:−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{15}}\right) \\ $$$$\therefore\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{15}}\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{15}}\right)}\:=\:\mathrm{1} \\ $$
