Question Number 91555 by mr W last updated on 01/May/20

Commented by jagoll last updated on 01/May/20
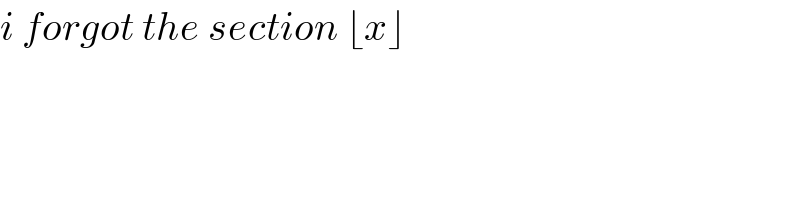
$${i}\:{forgot}\:{the}\:{section}\:\lfloor{x}\rfloor\: \\ $$
Commented by mathmax by abdo last updated on 01/May/20
![I=∫_0 ^1 (−1)^([(1/x)]) dx changement (1/x)=t give I =∫_1 ^∞ (−1)^([t]) (dt/t^2 ) =Σ_(n=1) ^∞ ∫_n ^(n+1) (((−1)^n )/t^2 )dt =Σ_(n=1) ^∞ (−1)^n [−(1/t)]_n ^(n+1) =Σ_(n=1) ^∞ (−1)^n ((1/n)−(1/(n+1))) =Σ_(n=1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/(n+1)) we have Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) Σ_(n=1) ^∞ (((−1)^n )/(n+1)) =Σ_(n=2) ^∞ (((−1)^(n−1) )/n) =−Σ_(n=2) ^∞ (((−1)^n )/n) =−(Σ_(n=1) ^∞ (((−1)^n )/n) +1) =−(−ln2 +1) =ln(2)−1 ⇒ I =−ln(2)−ln(2)+1 =1−2ln(2)](https://www.tinkutara.com/question/Q91583.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(−\mathrm{1}\right)^{\left[\frac{\mathrm{1}}{{x}}\right]} {dx}\:\:{changement}\:\frac{\mathrm{1}}{{x}}={t}\:{give} \\ $$$${I}\:=\int_{\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\left[{t}\right]} \frac{{dt}}{{t}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{t}^{\mathrm{2}} }{dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\left[−\frac{\mathrm{1}}{{t}}\right]_{{n}} ^{{n}+\mathrm{1}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}} \\ $$$${we}\:{have}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{2}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:=−\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}} \\ $$$$=−\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:+\mathrm{1}\right)\:=−\left(−{ln}\mathrm{2}\:+\mathrm{1}\right)\:={ln}\left(\mathrm{2}\right)−\mathrm{1}\:\Rightarrow \\ $$$${I}\:=−{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{2}\right)+\mathrm{1}\:=\mathrm{1}−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$
Commented by mr W last updated on 01/May/20

$${exact}!\:{thanks}\:{sir}! \\ $$
Commented by mathmax by abdo last updated on 01/May/20
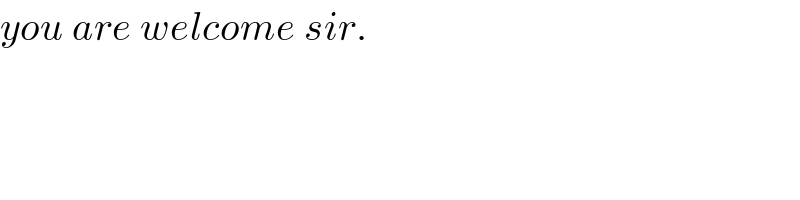
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by M±th+et+s last updated on 02/May/20
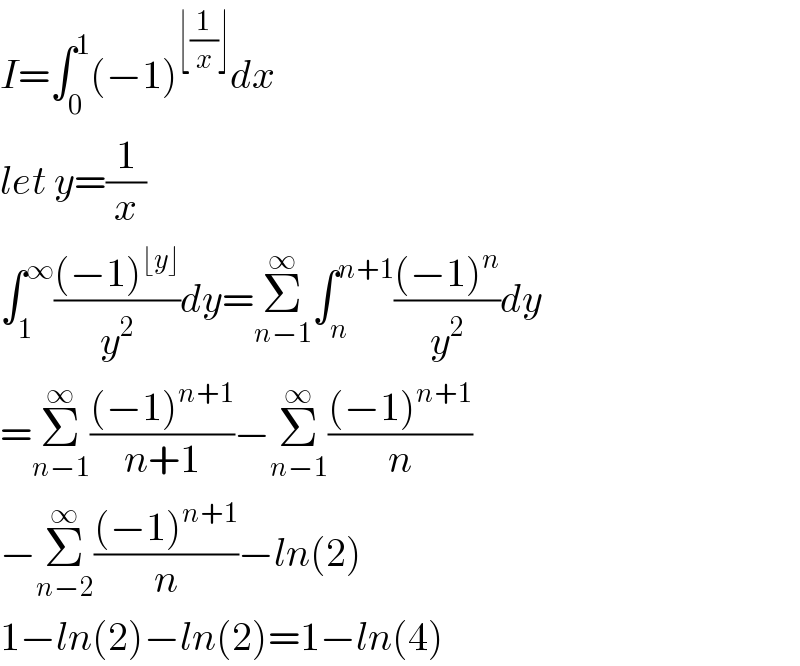
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{\lfloor\frac{\mathrm{1}}{{x}}\rfloor} {dx} \\ $$$${let}\:{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\lfloor{y}\rfloor} }{{y}^{\mathrm{2}} }{dy}=\underset{{n}−\mathrm{1}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{n}} }{{y}^{\mathrm{2}} }{dy} \\ $$$$=\underset{{n}−\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}−\underset{{n}−\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}} \\ $$$$−\underset{{n}−\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}−{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{1}−{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{2}\right)=\mathrm{1}−{ln}\left(\mathrm{4}\right) \\ $$
