Question Number 91568 by jagoll last updated on 01/May/20

Answered by MJS last updated on 01/May/20
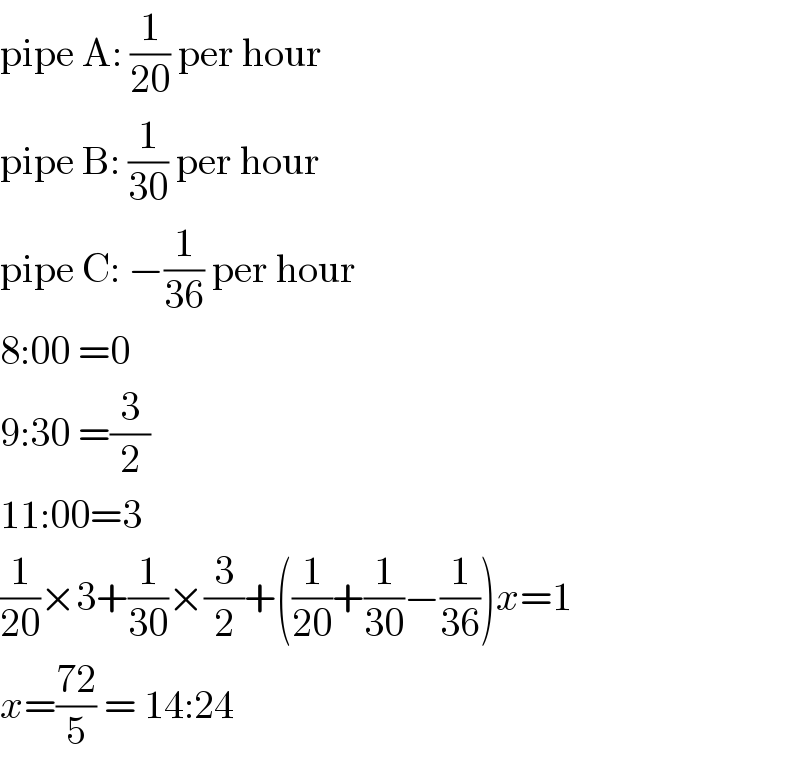
$$\mathrm{pipe}\:\mathrm{A}:\:\frac{\mathrm{1}}{\mathrm{20}}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{pipe}\:\mathrm{B}:\:\frac{\mathrm{1}}{\mathrm{30}}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{pipe}\:\mathrm{C}:\:−\frac{\mathrm{1}}{\mathrm{36}}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{8}:\mathrm{00}\:=\mathrm{0} \\ $$$$\mathrm{9}:\mathrm{30}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{11}:\mathrm{00}=\mathrm{3} \\ $$$$\frac{\mathrm{1}}{\mathrm{20}}×\mathrm{3}+\frac{\mathrm{1}}{\mathrm{30}}×\frac{\mathrm{3}}{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{30}}−\frac{\mathrm{1}}{\mathrm{36}}\right){x}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{72}}{\mathrm{5}}\:=\:\mathrm{14}:\mathrm{24} \\ $$
Commented by jagoll last updated on 01/May/20

$${thank}\:{you} \\ $$
Answered by som(math1967) last updated on 01/May/20

$${Afill}\:{in}\:\mathrm{3}{hr}=\frac{\mathrm{3}}{\mathrm{20}}\:{part}\:{of}\:{tank} \\ $$$${B}\:{fill}\:{in}\:\mathrm{1}\frac{\mathrm{1}}{\mathrm{2}}{hr}=\frac{\mathrm{1}}{\mathrm{30}}×\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{20}}{part}.. \\ $$$${at}\:\mathrm{11}{A}.{M}\:{tank}\:{fill}=\frac{\mathrm{3}}{\mathrm{20}}\:+\frac{\mathrm{1}}{\mathrm{20}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{part}.. \\ $$$${empty}\:{portion}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{4}}{\mathrm{5}}{part} \\ $$$${A},{B},{C}\:{together}\:{fill} \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{30}}\:−\frac{\mathrm{1}}{\mathrm{36}}=\frac{\mathrm{1}}{\mathrm{18}}\:{part} \\ $$$$\therefore{remaining}\:{part}\:{fill} \\ $$$$\:\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{18}=\mathrm{14}\frac{\mathrm{2}}{\mathrm{5}}{hours} \\ $$$$=\mathrm{14}{hr}\:\mathrm{24}{min}\:{ans} \\ $$$${option}\:\left({a}\right) \\ $$$$ \\ $$
Commented by jagoll last updated on 01/May/20

$${thank}\:{you} \\ $$
