Question Number 91624 by john santu last updated on 02/May/20
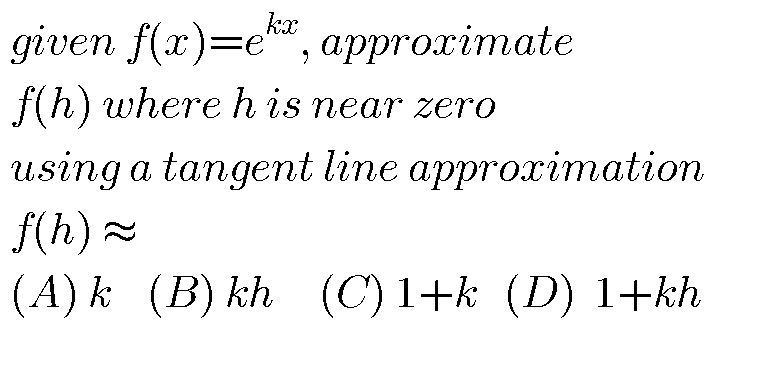
Commented by john santu last updated on 02/May/20

$${what}\:{the}\:{answer}? \\ $$
Commented by arcana last updated on 02/May/20
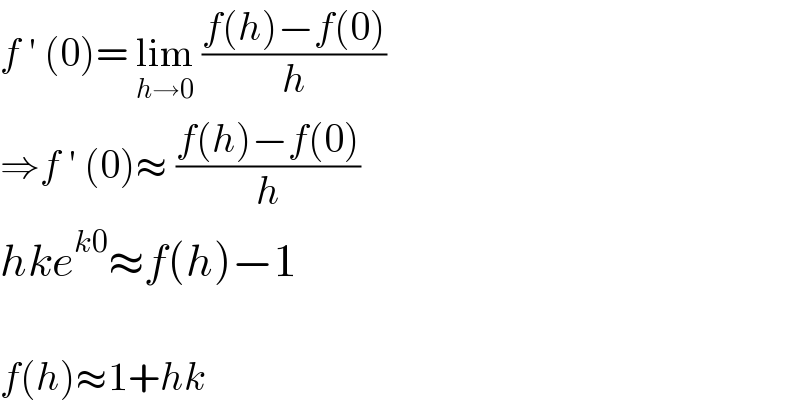
$${f}\:'\:\left(\mathrm{0}\right)=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({h}\right)−{f}\left(\mathrm{0}\right)}{{h}} \\ $$$$\Rightarrow{f}\:'\:\left(\mathrm{0}\right)\approx\:\frac{{f}\left({h}\right)−{f}\left(\mathrm{0}\right)}{{h}} \\ $$$${hke}^{{k}\mathrm{0}} \approx{f}\left({h}\right)−\mathrm{1} \\ $$$$ \\ $$$${f}\left({h}\right)\approx\mathrm{1}+{hk} \\ $$
Commented by mathmax by abdo last updated on 02/May/20
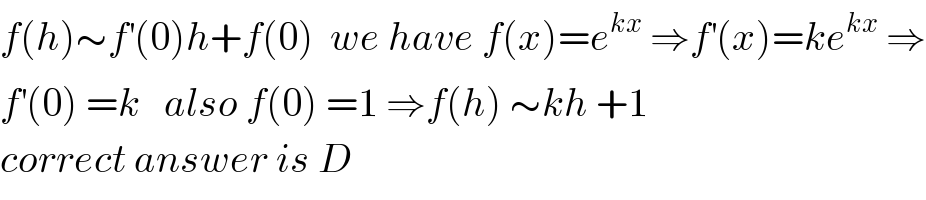
$${f}\left({h}\right)\sim{f}^{'} \left(\mathrm{0}\right){h}+{f}\left(\mathrm{0}\right)\:\:{we}\:{have}\:{f}\left({x}\right)={e}^{{kx}} \:\Rightarrow{f}^{'} \left({x}\right)={ke}^{{kx}} \:\Rightarrow \\ $$$${f}^{'} \left(\mathrm{0}\right)\:={k}\:\:\:{also}\:{f}\left(\mathrm{0}\right)\:=\mathrm{1}\:\Rightarrow{f}\left({h}\right)\:\sim{kh}\:+\mathrm{1} \\ $$$${correct}\:{answer}\:{is}\:{D} \\ $$
Commented by john santu last updated on 02/May/20
$${yes}.\:{i}\:{got}\:{same}\:{result}\: \\ $$
