Question Number 91656 by jagoll last updated on 02/May/20
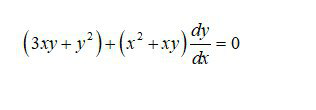
Commented by john santu last updated on 02/May/20
![(dy/dx) = ((−3xy−y^2 )/(x^2 +xy)) = ((−((3y)/x)−((y/x))^2 )/(1+((y/x)))) [ y = px ⇒ (dy/dx) = p + x(dp/dx) ] p +x (dp/dx) = ((−3p−p^2 )/(1+p)) x (dp/dx) = ((−4p−2p^2 )/(1+p)) (((1+p)dp)/(4p+2p^2 )) = −(dx/x) (((1+p)dp)/(2p(2+p))) = −(dx/x) ∫ (dp/(4p)) + ∫ (dp/(4(2+p))) = −ln x + C (1/4)ln(2p+p^2 ) = ln ((C/x)) ln(2p+p^2 ) = ln((C/x))^4 p^2 +2p+1= 1+((C/x))^4 ((y/x)+1)^2 = 1+((C/x))^4 y = x{−1 ± (√(1+((C/x))^4 ))}](https://www.tinkutara.com/question/Q91675.png)
$$\frac{{dy}}{{dx}}\:=\:\frac{−\mathrm{3}{xy}−{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{xy}}\:=\:\frac{−\frac{\mathrm{3}{y}}{{x}}−\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{y}}{{x}}\right)} \\ $$$$\left[\:{y}\:=\:{px}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{p}\:+\:{x}\frac{{dp}}{{dx}}\:\right] \\ $$$${p}\:+{x}\:\frac{{dp}}{{dx}}\:=\:\frac{−\mathrm{3}{p}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}} \\ $$$${x}\:\frac{{dp}}{{dx}}\:=\:\frac{−\mathrm{4}{p}−\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{1}+{p}} \\ $$$$\frac{\left(\mathrm{1}+{p}\right){dp}}{\mathrm{4}{p}+\mathrm{2}{p}^{\mathrm{2}} }\:=\:−\frac{{dx}}{{x}}\: \\ $$$$\frac{\left(\mathrm{1}+{p}\right){dp}}{\mathrm{2}{p}\left(\mathrm{2}+{p}\right)}\:=\:−\frac{{dx}}{{x}} \\ $$$$\int\:\frac{{dp}}{\mathrm{4}{p}}\:+\:\int\:\frac{{dp}}{\mathrm{4}\left(\mathrm{2}+{p}\right)}\:=\:−\mathrm{ln}\:{x}\:+\:{C}\:\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}{p}+{p}^{\mathrm{2}} \right)\:=\:\mathrm{ln}\:\left(\frac{\mathrm{C}}{{x}}\right) \\ $$$$\mathrm{ln}\left(\mathrm{2}{p}+{p}^{\mathrm{2}} \right)\:=\:\mathrm{ln}\left(\frac{\mathrm{C}}{{x}}\right)^{\mathrm{4}} \\ $$$${p}^{\mathrm{2}} +\mathrm{2}{p}+\mathrm{1}=\:\mathrm{1}+\left(\frac{{C}}{{x}}\right)^{\mathrm{4}} \\ $$$$\left(\frac{{y}}{{x}}+\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{1}+\left(\frac{{C}}{{x}}\right)^{\mathrm{4}} \\ $$$${y}\:=\:{x}\left\{−\mathrm{1}\:\pm\:\sqrt{\mathrm{1}+\left(\frac{{C}}{{x}}\right)^{\mathrm{4}} }\right\}\: \\ $$
Commented by jagoll last updated on 02/May/20

$${thank}\:{you} \\ $$
Answered by Kunal12588 last updated on 02/May/20
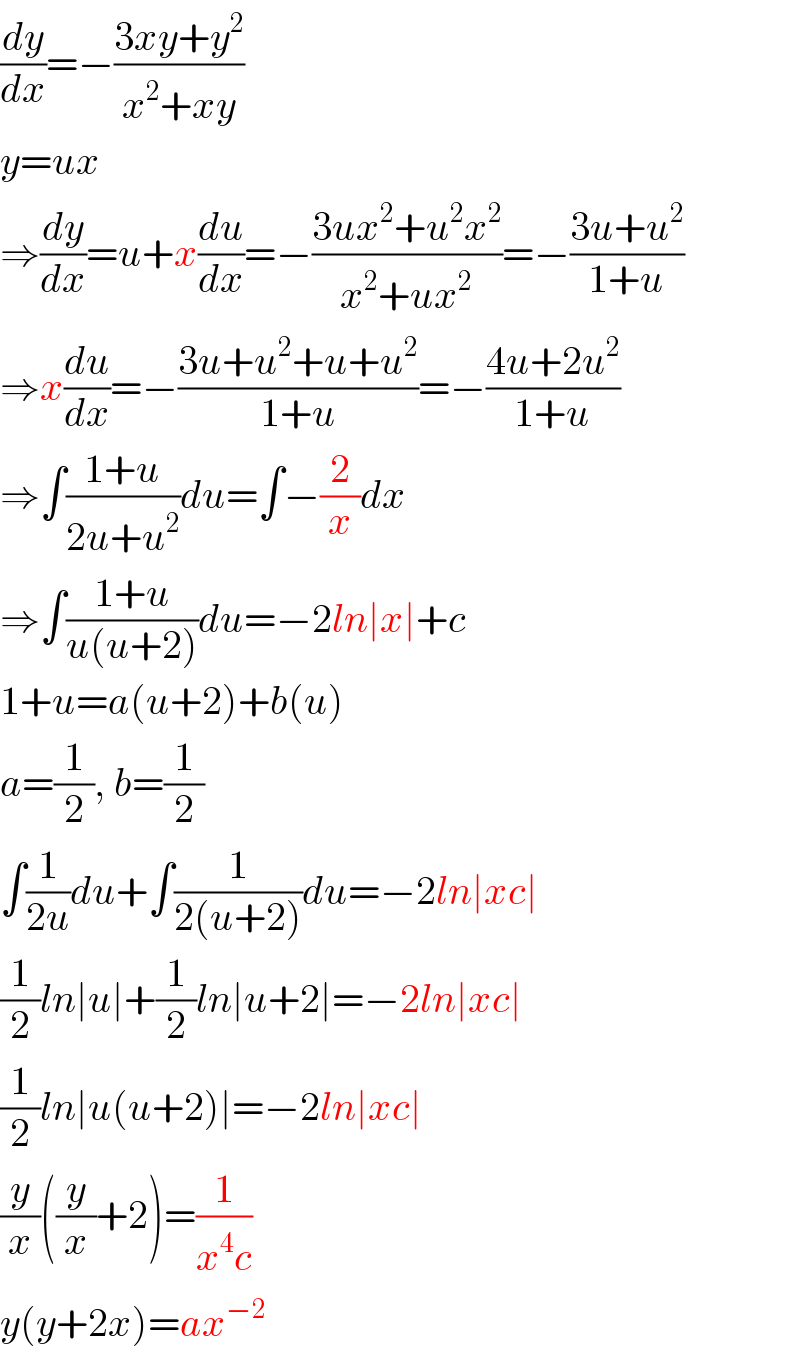
$$\frac{{dy}}{{dx}}=−\frac{\mathrm{3}{xy}+{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{xy}} \\ $$$${y}={ux} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={u}+{x}\frac{{du}}{{dx}}=−\frac{\mathrm{3}{ux}^{\mathrm{2}} +{u}^{\mathrm{2}} {x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{ux}^{\mathrm{2}} }=−\frac{\mathrm{3}{u}+{u}^{\mathrm{2}} }{\mathrm{1}+{u}} \\ $$$$\Rightarrow{x}\frac{{du}}{{dx}}=−\frac{\mathrm{3}{u}+{u}^{\mathrm{2}} +{u}+{u}^{\mathrm{2}} }{\mathrm{1}+{u}}=−\frac{\mathrm{4}{u}+\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{1}+{u}} \\ $$$$\Rightarrow\int\frac{\mathrm{1}+{u}}{\mathrm{2}{u}+{u}^{\mathrm{2}} }{du}=\int−\frac{\mathrm{2}}{{x}}{dx} \\ $$$$\Rightarrow\int\frac{\mathrm{1}+{u}}{{u}\left({u}+\mathrm{2}\right)}{du}=−\mathrm{2}{ln}\mid{x}\mid+{c} \\ $$$$\mathrm{1}+{u}={a}\left({u}+\mathrm{2}\right)+{b}\left({u}\right) \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}},\:{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}{u}}{du}+\int\frac{\mathrm{1}}{\mathrm{2}\left({u}+\mathrm{2}\right)}{du}=−\mathrm{2}{ln}\mid{xc}\mid \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}+\mathrm{2}\mid=−\mathrm{2}{ln}\mid{xc}\mid \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}\left({u}+\mathrm{2}\right)\mid=−\mathrm{2}{ln}\mid{xc}\mid \\ $$$$\frac{{y}}{{x}}\left(\frac{{y}}{{x}}+\mathrm{2}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{4}} {c}} \\ $$$${y}\left({y}+\mathrm{2}{x}\right)={ax}^{−\mathrm{2}} \\ $$
Commented by jagoll last updated on 02/May/20

$${wrong}\:{sir}\:{in}\:{line}\:\mathrm{3}\: \\ $$$$ \\ $$
