Question Number 91715 by 174 last updated on 02/May/20
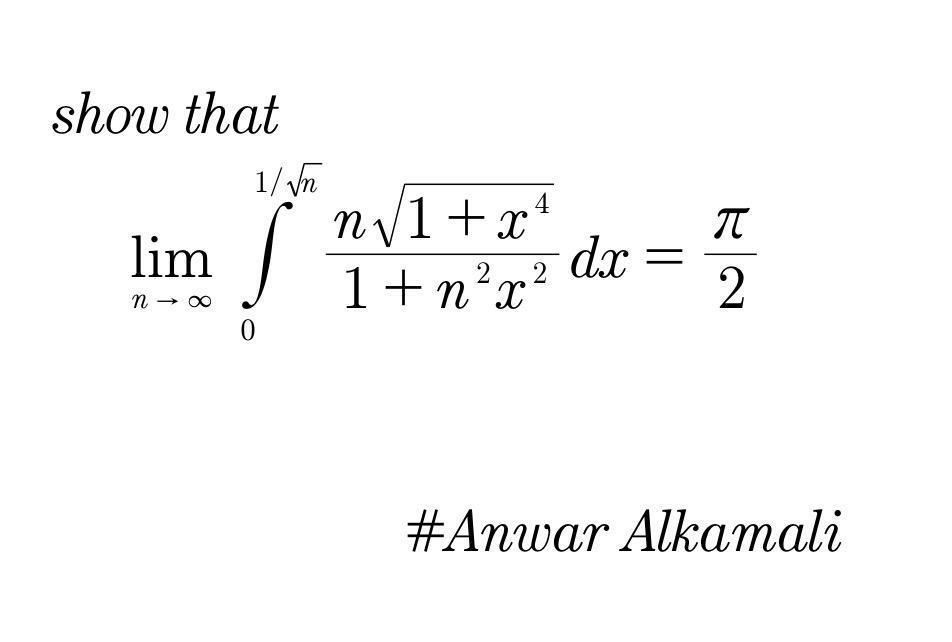
Commented by mathmax by abdo last updated on 02/May/20
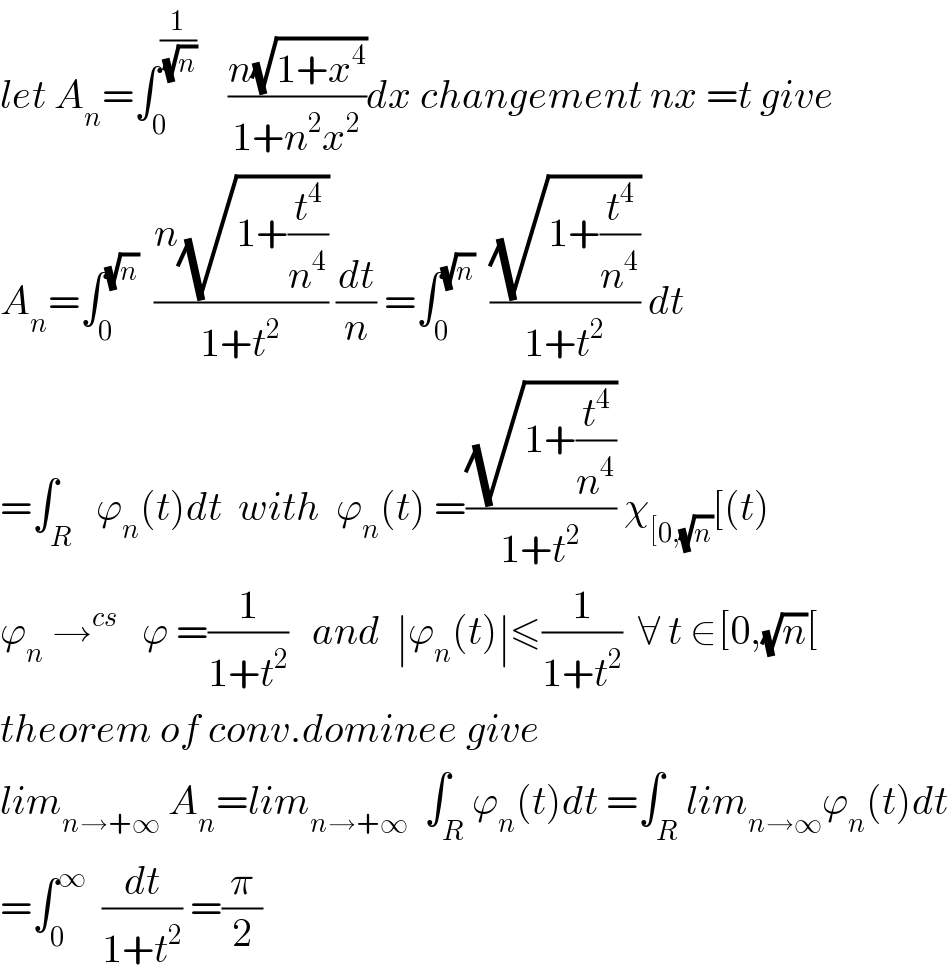
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{{n}}}} \:\:\:\:\frac{{n}\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}{\mathrm{1}+{n}^{\mathrm{2}} {x}^{\mathrm{2}} }{dx}\:{changement}\:{nx}\:={t}\:{give}\: \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\sqrt{{n}}} \:\:\frac{{n}\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{4}} }{{n}^{\mathrm{4}} }}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{{dt}}{{n}}\:=\int_{\mathrm{0}} ^{\sqrt{{n}}} \:\:\frac{\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{4}} }{{n}^{\mathrm{4}} }}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$=\int_{{R}} \:\:\varphi_{{n}} \left({t}\right){dt}\:\:{with}\:\:\varphi_{{n}} \left({t}\right)\:=\frac{\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{4}} }{{n}^{\mathrm{4}} }}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\chi_{\left[\mathrm{0},\sqrt{{n}}\right.} \left[\left({t}\right)\right. \\ $$$$\varphi_{{n}} \:\rightarrow^{{cs}} \:\:\:\varphi\:=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:{and}\:\:\mid\varphi_{{n}} \left({t}\right)\mid\leqslant\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\forall\:{t}\:\in\left[\mathrm{0},\sqrt{{n}}\left[\:\:\right.\right. \\ $$$${theorem}\:{of}\:{conv}.{dominee}\:{give} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} ={lim}_{{n}\rightarrow+\infty} \:\:\int_{{R}} \varphi_{{n}} \left({t}\right){dt}\:=\int_{{R}} {lim}_{{n}\rightarrow\infty} \varphi_{{n}} \left({t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}} \\ $$
Commented by 174 last updated on 02/May/20
thanks
Commented by abdomathmax last updated on 02/May/20

$${you}\:{are}\:{welcome}\:\: \\ $$
Commented by abdomathmax last updated on 02/May/20
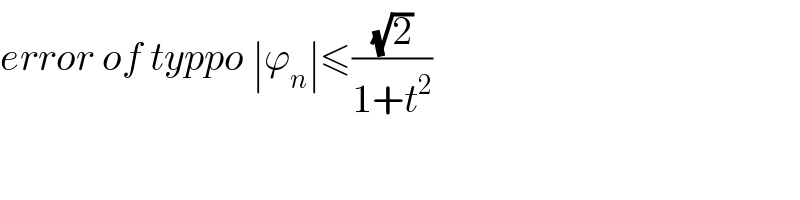
$${error}\:{of}\:{typpo}\:\mid\varphi_{{n}} \mid\leqslant\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$
