Question Number 91760 by M±th+et+s last updated on 02/May/20
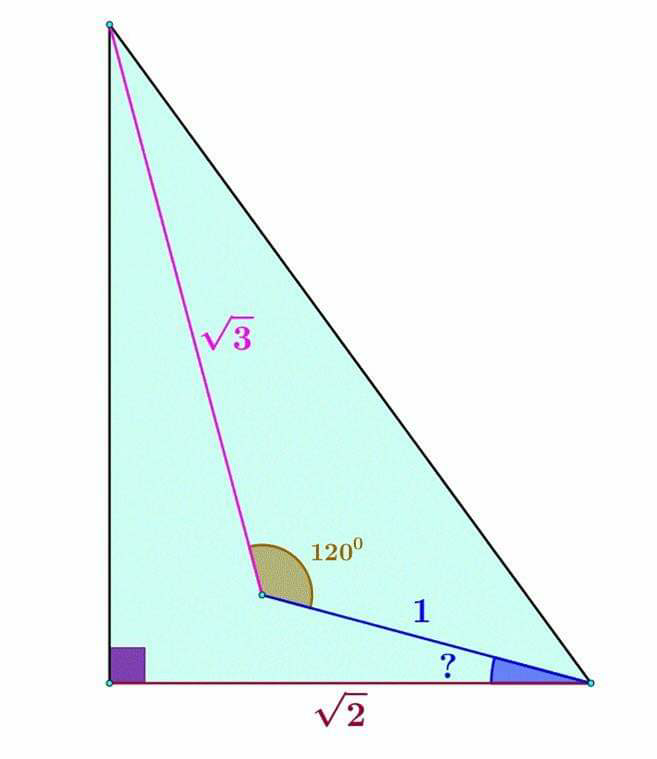
Commented by Tony Lin last updated on 03/May/20
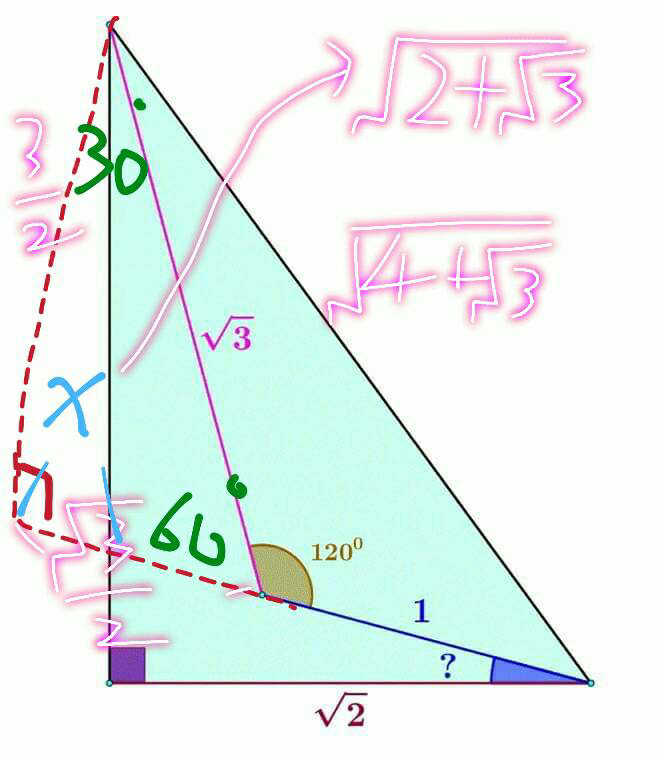
Commented by M±th+et+s last updated on 03/May/20
$${thanx}\:{for}\:{solutions} \\ $$
Commented by Tony Lin last updated on 03/May/20
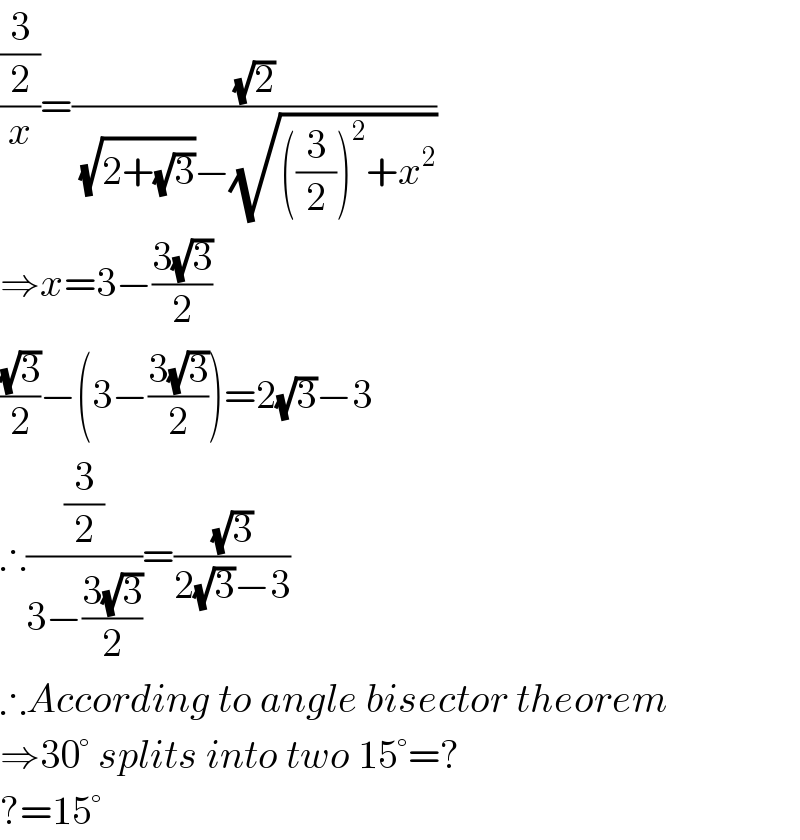
$$\frac{\frac{\mathrm{3}}{\mathrm{2}}}{{x}}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}−\sqrt{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow{x}=\mathrm{3}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(\mathrm{3}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$$\therefore\frac{\frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{3}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}} \\ $$$$\therefore{According}\:{to}\:{angle}\:{bisector}\:{theorem} \\ $$$$\Rightarrow\mathrm{30}°\:{splits}\:{into}\:{two}\:\mathrm{15}°=? \\ $$$$?=\mathrm{15}° \\ $$
Answered by mr W last updated on 03/May/20
Commented by mr W last updated on 03/May/20
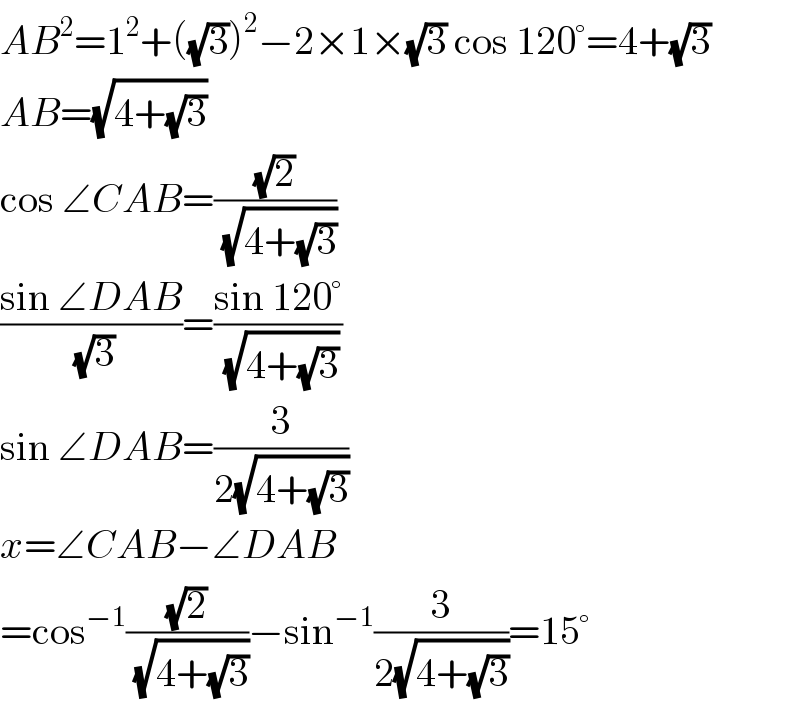
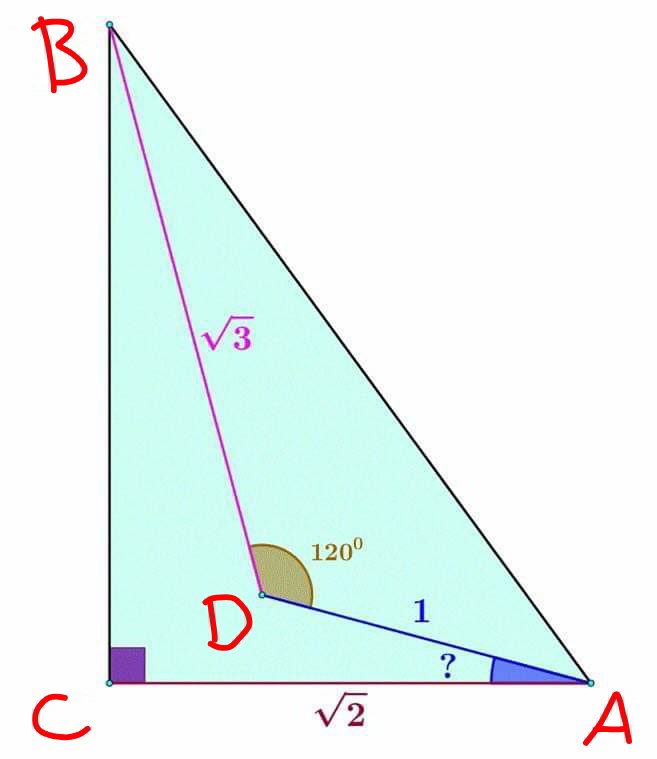
$${AB}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{120}°=\mathrm{4}+\sqrt{\mathrm{3}} \\ $$$${AB}=\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cos}\:\angle{CAB}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}}} \\ $$$$\frac{\mathrm{sin}\:\angle{DAB}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{sin}\:\mathrm{120}°}{\:\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}}} \\ $$$$\mathrm{sin}\:\angle{DAB}=\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}}} \\ $$$${x}=\angle{CAB}−\angle{DAB} \\ $$$$=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{4}+\sqrt{\mathrm{3}}}}=\mathrm{15}° \\ $$
