Question Number 91836 by M±th+et+s last updated on 03/May/20
Commented by M±th+et+s last updated on 03/May/20

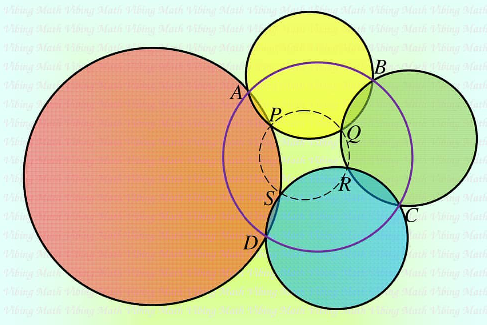
$${let}\:{A}\:{B}\:{C}\:{D}\:{be}\:{four}\:{points}\:{on}\:{a}\:{circle} \\ $$$${let}\:{four}\:{more}\:{cirvces}\:{pass}\:{through}\: \\ $$$${AB}\:,\:{BC}\:,\:{CD}\:,\:{DA}\:{Respectively}, \\ $$$${meeting}\:{infurther}\:{points}\:{P},{Q},{R},{S}. \\ $$$${show}\:{that}\:{P},{Q},{R}\:{and}\:{S}\:{are}\:{consyclic}. \\ $$
Answered by mr W last updated on 04/May/20
Commented by mr W last updated on 04/May/20
Commented by mr W last updated on 07/May/20
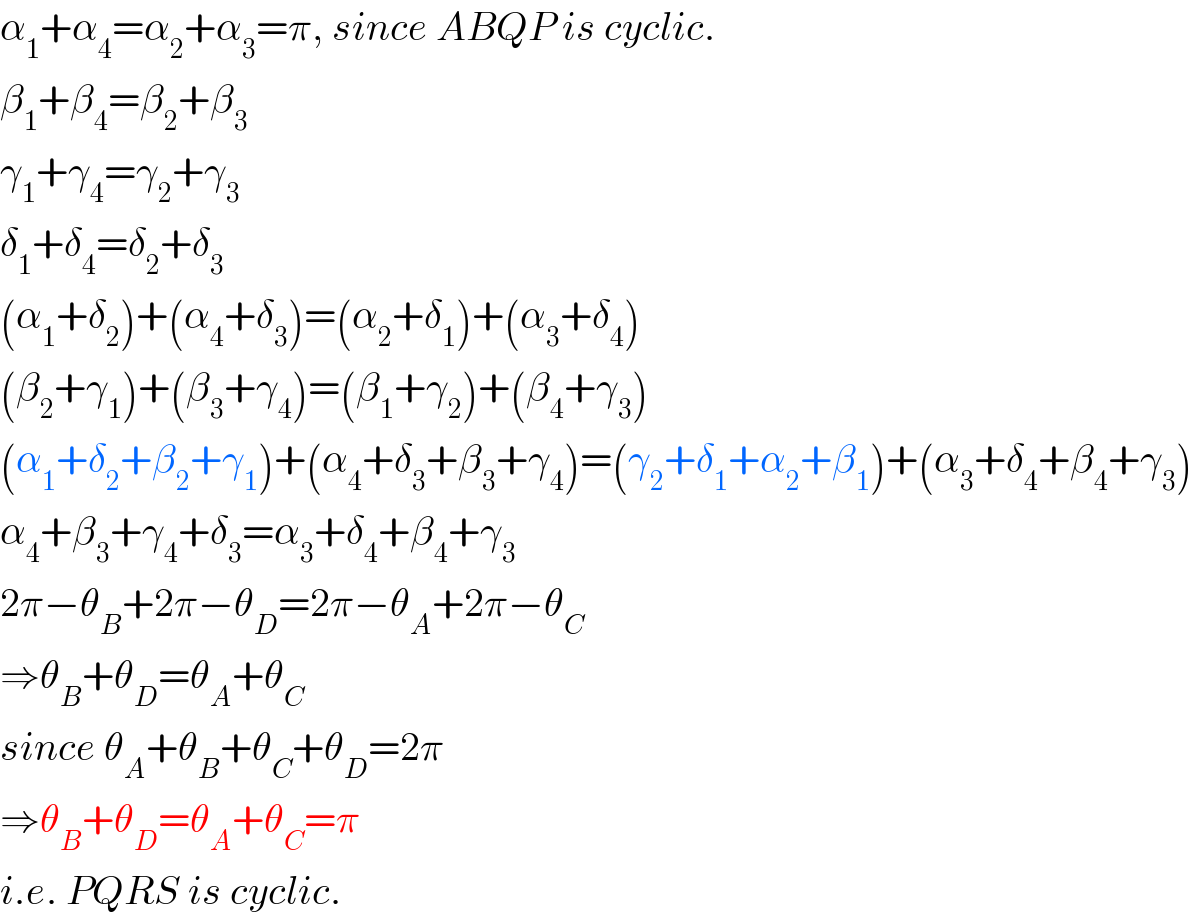
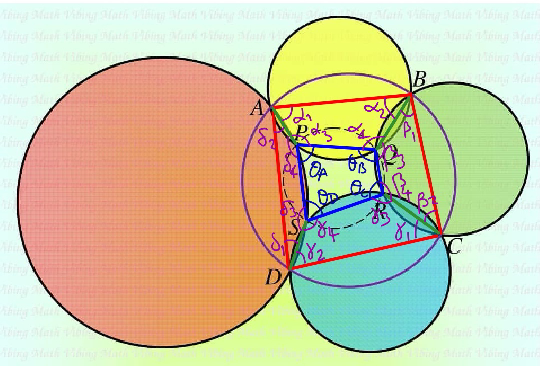
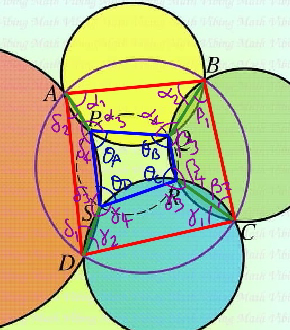
$$\alpha_{\mathrm{1}} +\alpha_{\mathrm{4}} =\alpha_{\mathrm{2}} +\alpha_{\mathrm{3}} =\pi,\:{since}\:{ABQP}\:{is}\:{cyclic}. \\ $$$$\beta_{\mathrm{1}} +\beta_{\mathrm{4}} =\beta_{\mathrm{2}} +\beta_{\mathrm{3}} \\ $$$$\gamma_{\mathrm{1}} +\gamma_{\mathrm{4}} =\gamma_{\mathrm{2}} +\gamma_{\mathrm{3}} \\ $$$$\delta_{\mathrm{1}} +\delta_{\mathrm{4}} =\delta_{\mathrm{2}} +\delta_{\mathrm{3}} \\ $$$$\left(\alpha_{\mathrm{1}} +\delta_{\mathrm{2}} \right)+\left(\alpha_{\mathrm{4}} +\delta_{\mathrm{3}} \right)=\left(\alpha_{\mathrm{2}} +\delta_{\mathrm{1}} \right)+\left(\alpha_{\mathrm{3}} +\delta_{\mathrm{4}} \right) \\ $$$$\left(\beta_{\mathrm{2}} +\gamma_{\mathrm{1}} \right)+\left(\beta_{\mathrm{3}} +\gamma_{\mathrm{4}} \right)=\left(\beta_{\mathrm{1}} +\gamma_{\mathrm{2}} \right)+\left(\beta_{\mathrm{4}} +\gamma_{\mathrm{3}} \right) \\ $$$$\left(\alpha_{\mathrm{1}} +\delta_{\mathrm{2}} +\beta_{\mathrm{2}} +\gamma_{\mathrm{1}} \right)+\left(\alpha_{\mathrm{4}} +\delta_{\mathrm{3}} +\beta_{\mathrm{3}} +\gamma_{\mathrm{4}} \right)=\left(\gamma_{\mathrm{2}} +\delta_{\mathrm{1}} +\alpha_{\mathrm{2}} +\beta_{\mathrm{1}} \right)+\left(\alpha_{\mathrm{3}} +\delta_{\mathrm{4}} +\beta_{\mathrm{4}} +\gamma_{\mathrm{3}} \right) \\ $$$$\alpha_{\mathrm{4}} +\beta_{\mathrm{3}} +\gamma_{\mathrm{4}} +\delta_{\mathrm{3}} =\alpha_{\mathrm{3}} +\delta_{\mathrm{4}} +\beta_{\mathrm{4}} +\gamma_{\mathrm{3}} \\ $$$$\mathrm{2}\pi−\theta_{{B}} +\mathrm{2}\pi−\theta_{{D}} =\mathrm{2}\pi−\theta_{{A}} +\mathrm{2}\pi−\theta_{{C}} \\ $$$$\Rightarrow\theta_{{B}} +\theta_{{D}} =\theta_{{A}} +\theta_{{C}} \\ $$$${since}\:\theta_{{A}} +\theta_{{B}} +\theta_{{C}} +\theta_{{D}} =\mathrm{2}\pi \\ $$$$\Rightarrow\theta_{{B}} +\theta_{{D}} =\theta_{{A}} +\theta_{{C}} =\pi \\ $$$${i}.{e}.\:{PQRS}\:{is}\:{cyclic}. \\ $$
Commented by M±th+et+s last updated on 04/May/20

$${great}\:{work}\:{sir} \\ $$
