Question Number 91850 by Power last updated on 03/May/20

Commented by mr W last updated on 03/May/20
$${you}\:{are}\:{back}!\:{the}\:{same}\:{questions}\:{seem} \\ $$$${to}\:{be}\:{back}\:{too}… \\ $$
Commented by mr W last updated on 03/May/20
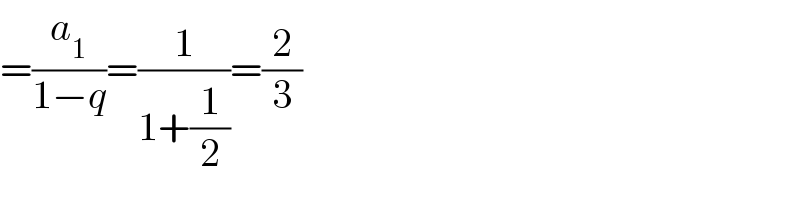
$$=\frac{{a}_{\mathrm{1}} }{\mathrm{1}−{q}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mathmax by abdo last updated on 03/May/20
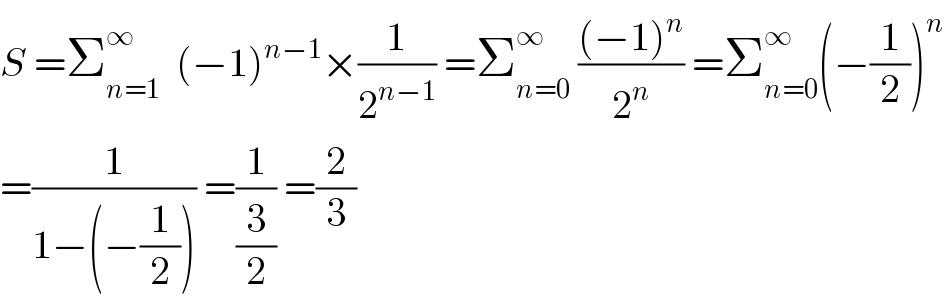
$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{2}}}\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
