Question Number 92084 by Power last updated on 04/May/20
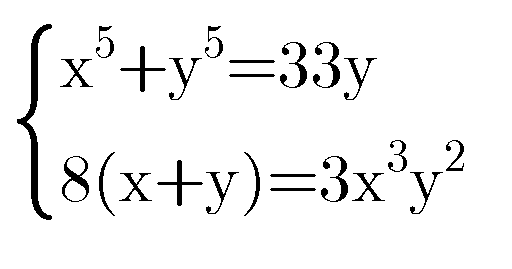
Answered by MJS last updated on 04/May/20

$$\mathrm{obviously}\:{x}_{\mathrm{0}} ={y}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{let}\:{x}\neq\mathrm{0}\:\wedge\:{y}={px}\:\wedge\:{p}\neq\mathrm{0} \\ $$$$\begin{cases}{{x}\left(\left({p}^{\mathrm{5}} +\mathrm{1}\right){x}^{\mathrm{4}} −\mathrm{33}{p}\right)=\mathrm{0}}\\{{x}\left(\mathrm{3}{p}^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{8}\left({p}+\mathrm{1}\right)\right)=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{{x}^{\mathrm{4}} =\frac{\mathrm{33}{p}}{{p}^{\mathrm{5}} +\mathrm{1}}}\\{{x}^{\mathrm{4}} =\frac{\mathrm{8}\left({p}+\mathrm{1}\right)}{\mathrm{3}{p}\mathrm{2}}}\end{cases} \\ $$$$\Rightarrow \\ $$$${p}^{\mathrm{6}} +{p}^{\mathrm{5}} −\frac{\mathrm{99}}{\mathrm{8}}{p}^{\mathrm{3}} +{p}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{I}\:\mathrm{found} \\ $$$$\left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({p}−\mathrm{2}\right)\left({p}^{\mathrm{4}} +\frac{\mathrm{7}}{\mathrm{2}}{p}^{\mathrm{3}} +\frac{\mathrm{31}}{\mathrm{4}}{p}^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{2}}{p}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}_{\mathrm{2}} =\mathrm{2} \\ $$$${p}_{\mathrm{3},\:\mathrm{4}} =−\frac{\mathrm{7}}{\mathrm{8}}+\frac{\sqrt{−\mathrm{29}+\mathrm{2}\sqrt{\mathrm{737}}}}{\mathrm{8}}\pm\left(\frac{\sqrt{\mathrm{43}}}{\mathrm{8}}−\frac{\sqrt{\mathrm{29}+\mathrm{2}\sqrt{\mathrm{737}}}}{\mathrm{8}}\right)\mathrm{i} \\ $$$${p}_{\mathrm{5},\:\mathrm{6}} =−\frac{\mathrm{7}}{\mathrm{8}}−\frac{\sqrt{−\mathrm{29}+\mathrm{2}\sqrt{\mathrm{737}}}}{\mathrm{8}}\pm\left(\frac{\sqrt{\mathrm{43}}}{\mathrm{8}}+\frac{\sqrt{\mathrm{29}+\mathrm{2}\sqrt{\mathrm{737}}}}{\mathrm{8}}\right)\mathrm{i} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{be}\:\mathrm{so}\:\mathrm{kind}\:\mathrm{and}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{rest}… \\ $$
Commented by Power last updated on 05/May/20

$$\mathrm{thanks} \\ $$
