Question Number 92115 by mhmd last updated on 04/May/20
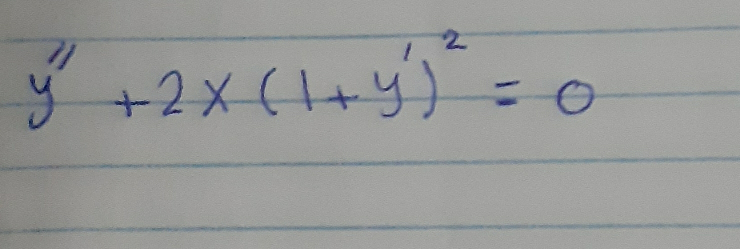
Answered by mr W last updated on 05/May/20
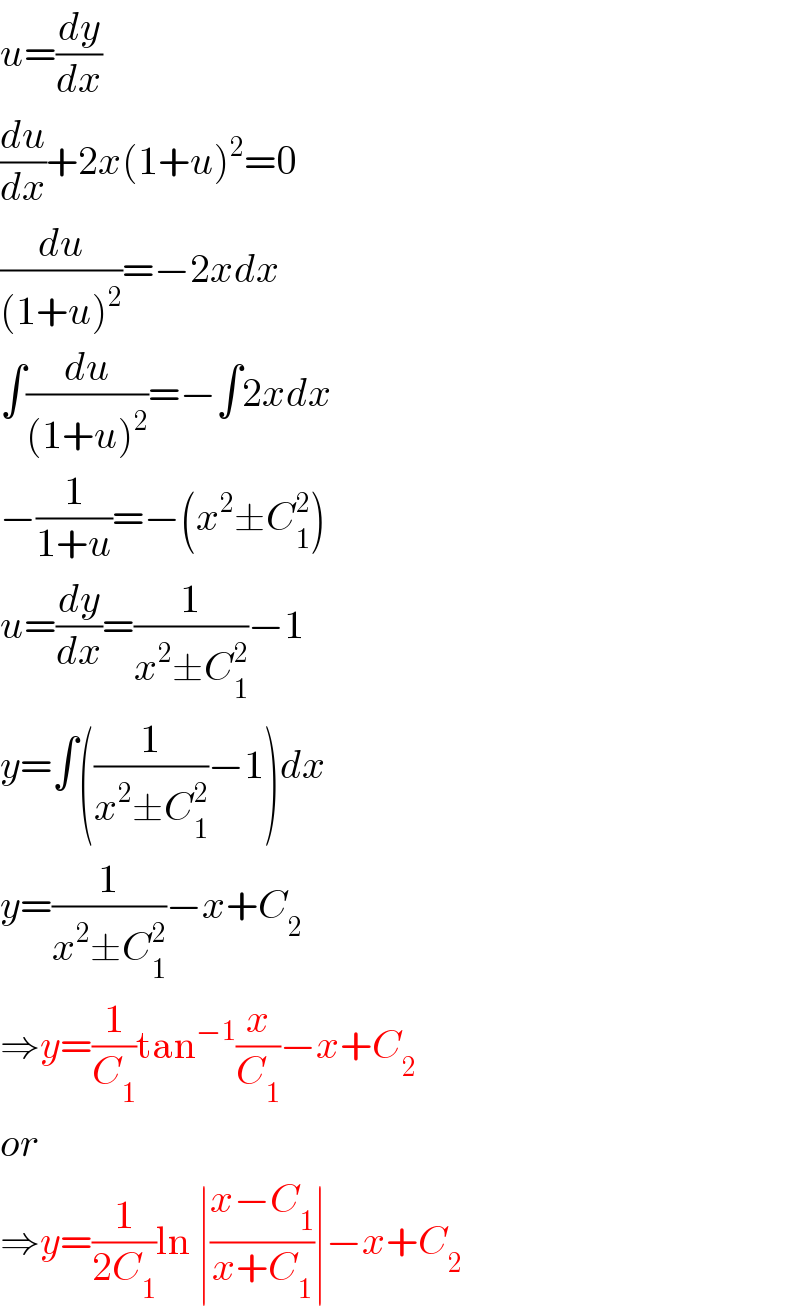
$${u}=\frac{{dy}}{{dx}} \\ $$$$\frac{{du}}{{dx}}+\mathrm{2}{x}\left(\mathrm{1}+{u}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }=−\mathrm{2}{xdx} \\ $$$$\int\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }=−\int\mathrm{2}{xdx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{1}+{u}}=−\left({x}^{\mathrm{2}} \pm{C}_{\mathrm{1}} ^{\mathrm{2}} \right) \\ $$$${u}=\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \pm{C}_{\mathrm{1}} ^{\mathrm{2}} }−\mathrm{1} \\ $$$${y}=\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} \pm{C}_{\mathrm{1}} ^{\mathrm{2}} }−\mathrm{1}\right){dx} \\ $$$${y}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \pm{C}_{\mathrm{1}} ^{\mathrm{2}} }−{x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{{C}_{\mathrm{1}} }\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{{C}_{\mathrm{1}} }−{x}+{C}_{\mathrm{2}} \\ $$$${or} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{2}{C}_{\mathrm{1}} }\mathrm{ln}\:\mid\frac{{x}−{C}_{\mathrm{1}} }{{x}+{C}_{\mathrm{1}} }\mid−{x}+{C}_{\mathrm{2}} \\ $$
