Question Number 92219 by ajfour last updated on 05/May/20

Commented by ajfour last updated on 05/May/20

$${If}\:{the}\:{red}\:{curve}\:{has}\:{equation} \\ $$$${y}={x}^{\mathrm{2}} −{bx}+{c}=\mathrm{0}\:\:\forall\:\:{b},\:{c}\:>\mathrm{0}\:,\:{then} \\ $$$${find}\:{equation}\:{of}\:{upper}\:{cubic} \\ $$$${in}\:{the}\:{form}\:{y}={px}^{\mathrm{3}} +{qx}+{r}. \\ $$$${Hence}\:{find}\:\frac{{q}}{{p}},\:\frac{{r}}{{p}}\:. \\ $$$${Thus}\:{we}\:{can}\:{determine}\:{the} \\ $$$${common}\:{root}\:{by}\:{using}\:{just} \\ $$$${tbe}\:{Cardano}\:{formula}. \\ $$$${hence}\:{all}\:{the}\:{roots}\:{of}\:{the}\:{red} \\ $$$${cubic}\:{curve}\:{even}\:{when}\:{the} \\ $$$${discriminant}:\:\:\:\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{{b}^{\mathrm{3}} }{\mathrm{27}}\:<\:\mathrm{0}\:. \\ $$
Commented by ajfour last updated on 05/May/20
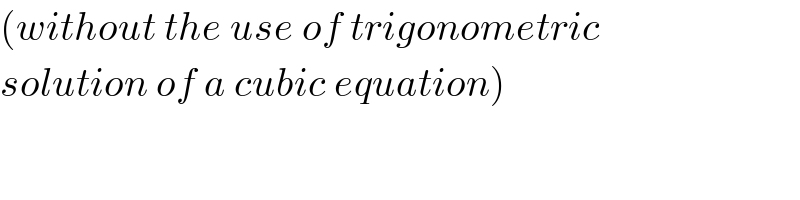
$$\left({without}\:{the}\:{use}\:{of}\:{trigonometric}\right. \\ $$$$\left.{solution}\:{of}\:{a}\:{cubic}\:{equation}\right) \\ $$
Commented by ajfour last updated on 05/May/20
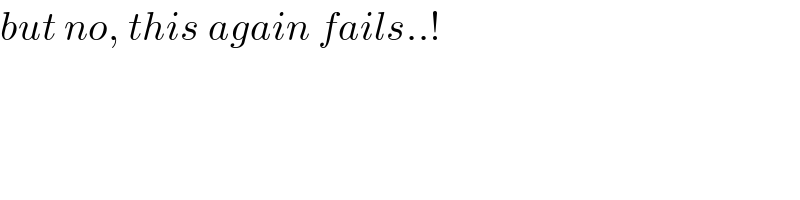
$${but}\:{no},\:{this}\:{again}\:{fails}..! \\ $$
Commented by MJS last updated on 05/May/20

$$\mathrm{anyway},\:\mathrm{the}\:\mathrm{black}\:\mathrm{curve}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique} \\ $$
Commented by ajfour last updated on 06/May/20
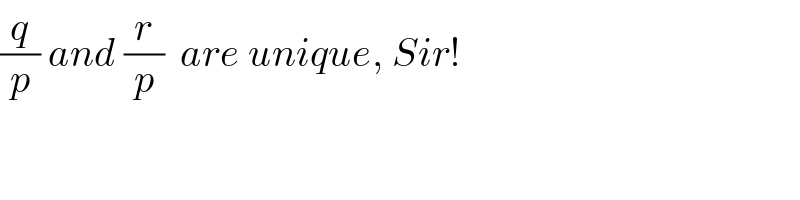
$$\frac{{q}}{{p}}\:{and}\:\frac{{r}}{{p}}\:\:{are}\:{unique},\:{Sir}! \\ $$
