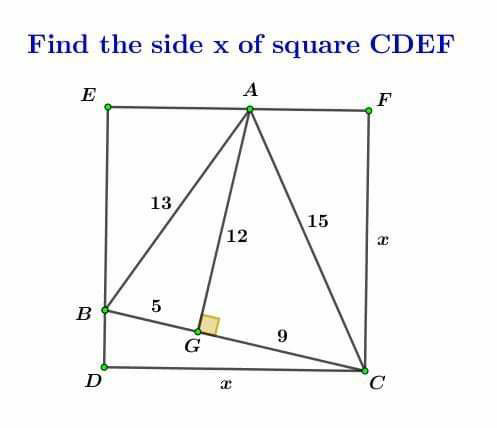
Question Number 92248 by naka3546 last updated on 05/May/20
Commented by MJS last updated on 06/May/20
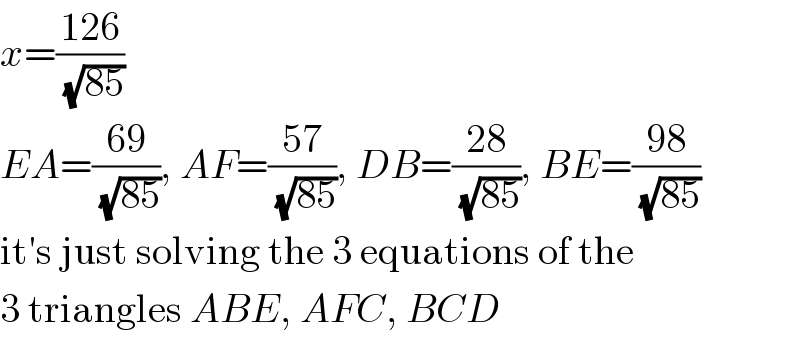
$${x}=\frac{\mathrm{126}}{\:\sqrt{\mathrm{85}}} \\ $$$${EA}=\frac{\mathrm{69}}{\:\sqrt{\mathrm{85}}},\:{AF}=\frac{\mathrm{57}}{\:\sqrt{\mathrm{85}}},\:{DB}=\frac{\mathrm{28}}{\:\sqrt{\mathrm{85}}},\:{BE}=\frac{\mathrm{98}}{\:\sqrt{\mathrm{85}}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{solving}\:\mathrm{the}\:\mathrm{3}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{3}\:\mathrm{triangles}\:{ABE},\:{AFC},\:{BCD} \\ $$
Commented by Prithwish Sen 1 last updated on 06/May/20
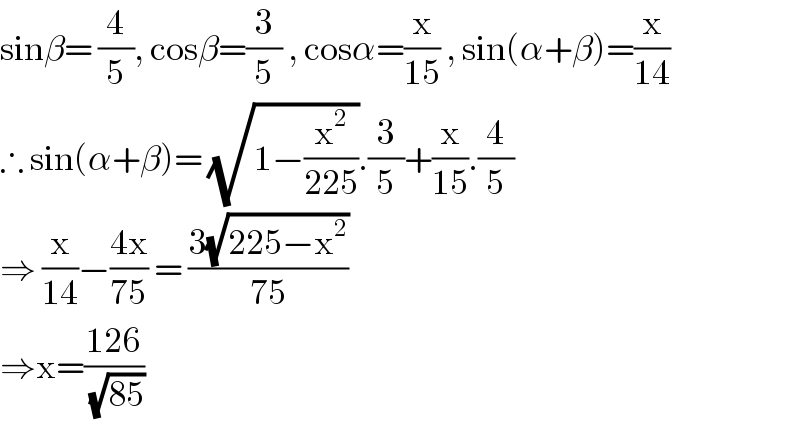
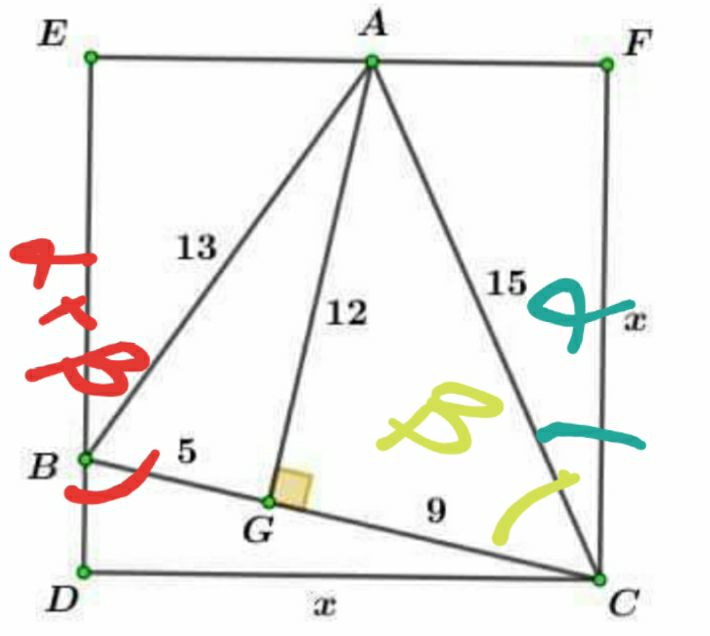
$$\mathrm{sin}\beta=\:\frac{\mathrm{4}}{\mathrm{5}},\:\mathrm{cos}\beta=\frac{\mathrm{3}}{\mathrm{5}}\:,\:\mathrm{cos}\alpha=\frac{\mathrm{x}}{\mathrm{15}}\:,\:\mathrm{sin}\left(\alpha+\beta\right)=\frac{\mathrm{x}}{\mathrm{14}} \\ $$$$\therefore\:\mathrm{sin}\left(\alpha+\beta\right)=\:\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{225}}}.\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{x}}{\mathrm{15}}.\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\:\frac{\mathrm{x}}{\mathrm{14}}−\frac{\mathrm{4x}}{\mathrm{75}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{225}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{75}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{126}}{\:\sqrt{\mathrm{85}}} \\ $$
Commented by Prithwish Sen 1 last updated on 06/May/20
Commented by naka3546 last updated on 08/May/20
$${Thank}\:\:{you}\:,\:\:{sir}\:. \\ $$
