Menu Close

Question-92717

Tinku Tara 0 Comments
Pin




Question Number 92717 by mr W last updated on 08/May/20
Commented by i jagooll last updated on 09/May/20
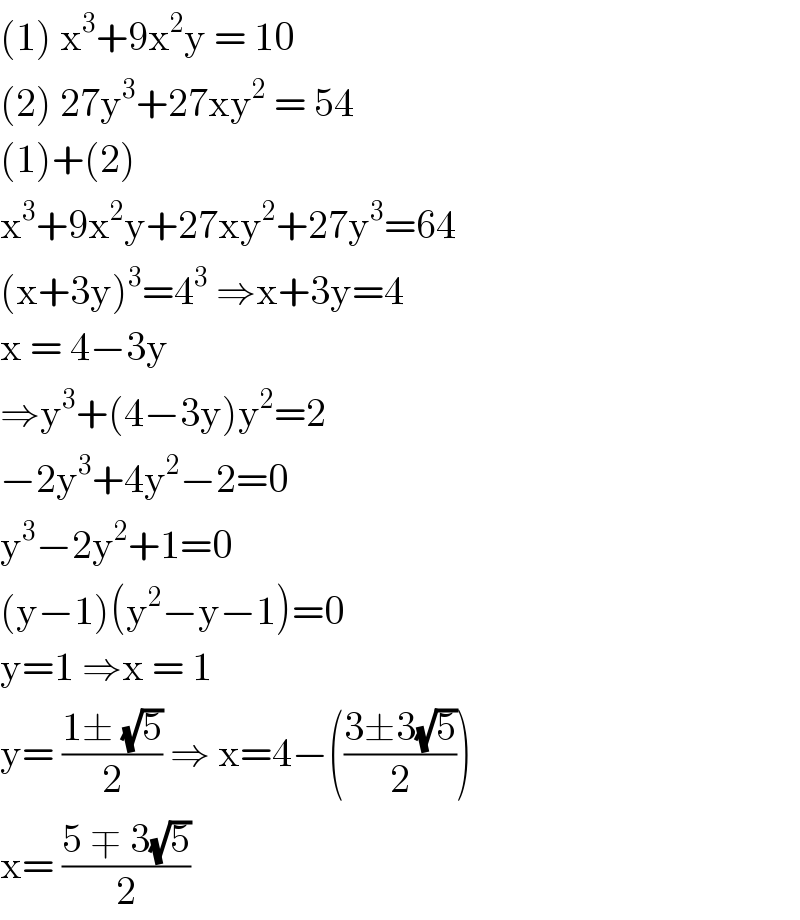
(1) x^3 +9x^2 y = 10 (2) 27y^3 +27xy^2 = 54 (1)+(2) x^3 +9x^2 y+27xy^2 +27y^3 =64 (x+3y)^3 =4^3 ⇒x+3y=4 x = 4−3y ⇒y^3 +(4−3y)y^2 =2 −2y^3 +4y^2 −2=0 y^3 −2y^2 +1=0 (y−1)(y^2 −y−1)=0 y=1 ⇒x = 1 y= ((1± (√5))/2) ⇒ x=4−(((3±3(√5))/2)) x= ((5 ∓ 3(√5))/2)
$$\left(\mathrm{1}\right)\:\mathrm{x}^{\mathrm{3}} +\mathrm{9x}^{\mathrm{2}} \mathrm{y}\:=\:\mathrm{10} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{27y}^{\mathrm{3}} +\mathrm{27xy}^{\mathrm{2}} \:=\:\mathrm{54} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{9x}^{\mathrm{2}} \mathrm{y}+\mathrm{27xy}^{\mathrm{2}} +\mathrm{27y}^{\mathrm{3}} =\mathrm{64} \\ $$$$\left(\mathrm{x}+\mathrm{3y}\right)^{\mathrm{3}} =\mathrm{4}^{\mathrm{3}} \:\Rightarrow\mathrm{x}+\mathrm{3y}=\mathrm{4} \\ $$$$\mathrm{x}\:=\:\mathrm{4}−\mathrm{3y} \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{3}} +\left(\mathrm{4}−\mathrm{3y}\right)\mathrm{y}^{\mathrm{2}} =\mathrm{2} \\ $$$$−\mathrm{2y}^{\mathrm{3}} +\mathrm{4y}^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{3}} −\mathrm{2y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{y}=\mathrm{1}\:\Rightarrow\mathrm{x}\:=\:\mathrm{1} \\ $$$$\mathrm{y}=\:\frac{\mathrm{1}\pm\:\sqrt{\mathrm{5}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{x}=\mathrm{4}−\left(\frac{\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\mathrm{x}=\:\frac{\mathrm{5}\:\mp\:\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}\: \\ $$
Commented by mr W last updated on 09/May/20
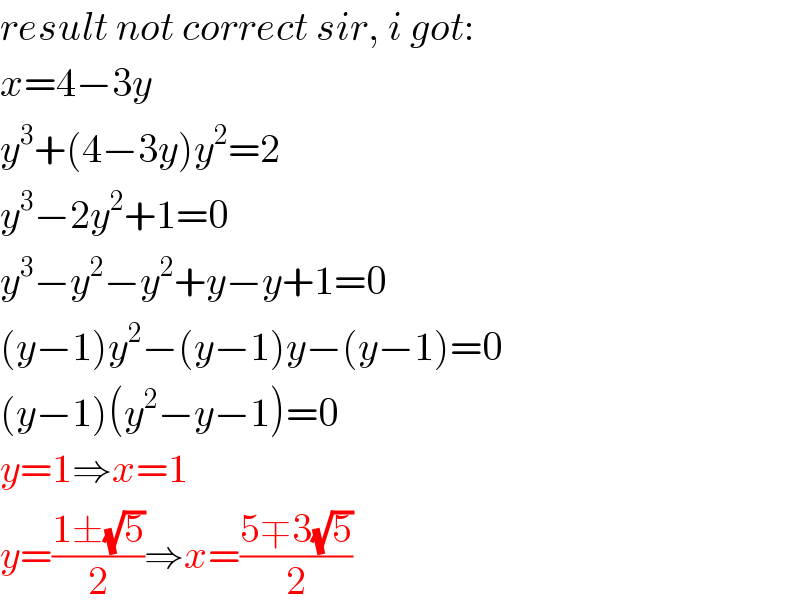
result not correct sir, i got: x=4−3y y^3 +(4−3y)y^2 =2 y^3 −2y^2 +1=0 y^3 −y^2 −y^2 +y−y+1=0 (y−1)y^2 −(y−1)y−(y−1)=0 (y−1)(y^2 −y−1)=0 y=1⇒x=1 y=((1±(√5))/2)⇒x=((5∓3(√5))/2)
$${result}\:{not}\:{correct}\:{sir},\:{i}\:{got}: \\ $$$${x}=\mathrm{4}−\mathrm{3}{y} \\ $$$${y}^{\mathrm{3}} +\left(\mathrm{4}−\mathrm{3}{y}\right){y}^{\mathrm{2}} =\mathrm{2} \\ $$$${y}^{\mathrm{3}} −\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} −{y}^{\mathrm{2}} −{y}^{\mathrm{2}} +{y}−{y}+\mathrm{1}=\mathrm{0} \\ $$$$\left({y}−\mathrm{1}\right){y}^{\mathrm{2}} −\left({y}−\mathrm{1}\right){y}−\left({y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({y}−\mathrm{1}\right)\left({y}^{\mathrm{2}} −{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}=\mathrm{1}\Rightarrow{x}=\mathrm{1} \\ $$$${y}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow{x}=\frac{\mathrm{5}\mp\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by i jagooll last updated on 09/May/20
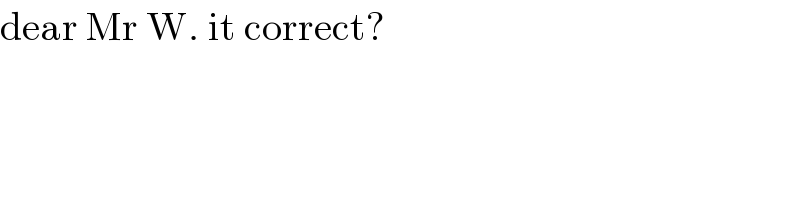
dear Mr W. it correct?
$$\mathrm{dear}\:\mathrm{Mr}\:\mathrm{W}.\:\mathrm{it}\:\mathrm{correct}? \\ $$
Commented by i jagooll last updated on 09/May/20
o yes sir. i typo
$$\mathrm{o}\:\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{typo}\: \\ $$
Commented by john santu last updated on 09/May/20
greeatm..������
Answered by Rasheed.Sindhi last updated on 08/May/20
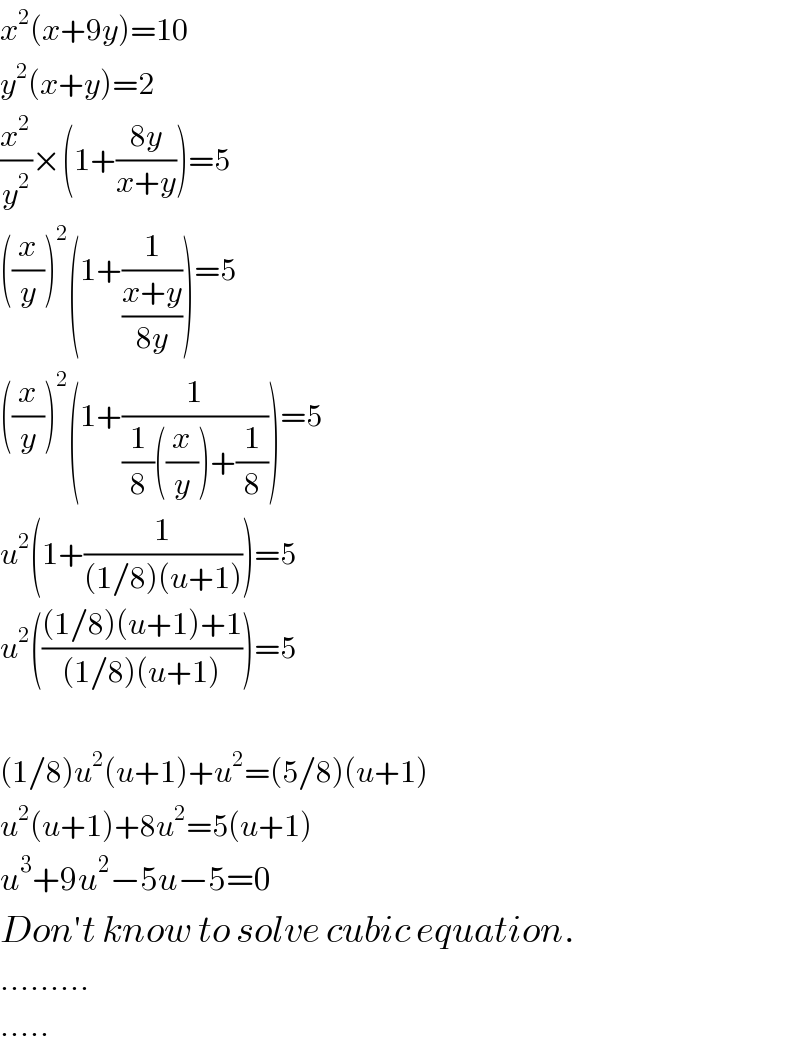
x^2 (x+9y)=10 y^2 (x+y)=2 (x^2 /y^2 )×(1+((8y)/(x+y)))=5 ((x/y))^2 (1+(1/((x+y)/(8y))))=5 ((x/y))^2 (1+(1/((1/8)((x/y))+(1/8))))=5 u^2 (1+(1/((1/8)(u+1))))=5 u^2 ((((1/8)(u+1)+1)/((1/8)(u+1))))=5 (1/8)u^2 (u+1)+u^2 =(5/8)(u+1) u^2 (u+1)+8u^2 =5(u+1) u^3 +9u^2 −5u−5=0 Don′t know to solve cubic equation. ......... .....
$${x}^{\mathrm{2}} \left({x}+\mathrm{9}{y}\right)=\mathrm{10} \\ $$$${y}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{2} \\ $$$$\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }×\left(\mathrm{1}+\frac{\mathrm{8}{y}}{{x}+{y}}\right)=\mathrm{5} \\ $$$$\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\frac{{x}+{y}}{\mathrm{8}{y}}}\right)=\mathrm{5} \\ $$$$\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{{x}}{{y}}\right)+\frac{\mathrm{1}}{\mathrm{8}}}\right)=\mathrm{5} \\ $$$${u}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{1}/\mathrm{8}\right)\left({u}+\mathrm{1}\right)}\right)=\mathrm{5} \\ $$$${u}^{\mathrm{2}} \left(\frac{\left(\mathrm{1}/\mathrm{8}\right)\left({u}+\mathrm{1}\right)+\mathrm{1}}{\left(\mathrm{1}/\mathrm{8}\right)\left({u}+\mathrm{1}\right)}\right)=\mathrm{5} \\ $$$$ \\ $$$$\left(\mathrm{1}/\mathrm{8}\right){u}^{\mathrm{2}} \left({u}+\mathrm{1}\right)+{u}^{\mathrm{2}} =\left(\mathrm{5}/\mathrm{8}\right)\left({u}+\mathrm{1}\right) \\ $$$${u}^{\mathrm{2}} \left({u}+\mathrm{1}\right)+\mathrm{8}{u}^{\mathrm{2}} =\mathrm{5}\left({u}+\mathrm{1}\right) \\ $$$${u}^{\mathrm{3}} +\mathrm{9}{u}^{\mathrm{2}} −\mathrm{5}{u}−\mathrm{5}=\mathrm{0} \\ $$$${Don}'{t}\:{know}\:{to}\:{solve}\:{cubic}\:{equation}. \\ $$$$……… \\ $$$$….. \\ $$
Commented by Rio Michael last updated on 08/May/20
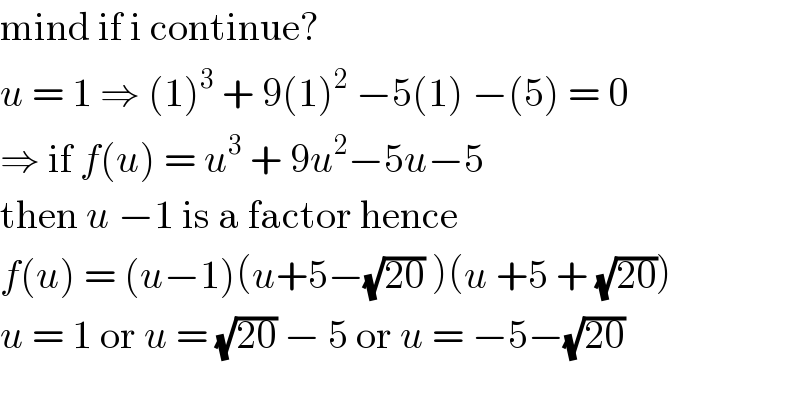
mind if i continue? u = 1 ⇒ (1)^3 + 9(1)^2 −5(1) −(5) = 0 ⇒ if f(u) = u^3 + 9u^2 −5u−5 then u −1 is a factor hence f(u) = (u−1)(u+5−(√(20)) )(u +5 + (√(20))) u = 1 or u = (√(20)) − 5 or u = −5−(√(20))
$$\mathrm{mind}\:\mathrm{if}\:\mathrm{i}\:\mathrm{continue}? \\ $$$${u}\:=\:\mathrm{1}\:\Rightarrow\:\left(\mathrm{1}\right)^{\mathrm{3}} \:+\:\mathrm{9}\left(\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{5}\left(\mathrm{1}\right)\:−\left(\mathrm{5}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{if}\:{f}\left({u}\right)\:=\:{u}^{\mathrm{3}} \:+\:\mathrm{9}{u}^{\mathrm{2}} −\mathrm{5}{u}−\mathrm{5} \\ $$$$\mathrm{then}\:{u}\:−\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{hence} \\ $$$${f}\left({u}\right)\:=\:\left({u}−\mathrm{1}\right)\left({u}+\mathrm{5}−\sqrt{\mathrm{20}}\:\right)\left({u}\:+\mathrm{5}\:+\:\sqrt{\mathrm{20}}\right)\: \\ $$$${u}\:=\:\mathrm{1}\:\mathrm{or}\:{u}\:=\:\sqrt{\mathrm{20}}\:−\:\mathrm{5}\:\mathrm{or}\:{u}\:=\:−\mathrm{5}−\sqrt{\mathrm{20}} \\ $$$$ \\ $$
Commented by mr W last updated on 08/May/20
thank you both!
$${thank}\:{you}\:{both}! \\ $$
Commented by Ar Brandon last updated on 09/May/20
�� I love this spirit. Keep up Men.��
Commented by Rasheed.Sindhi last updated on 13/May/20
7ank5 5ir for encouraging!
Answered by $@ty@m123 last updated on 10/May/20
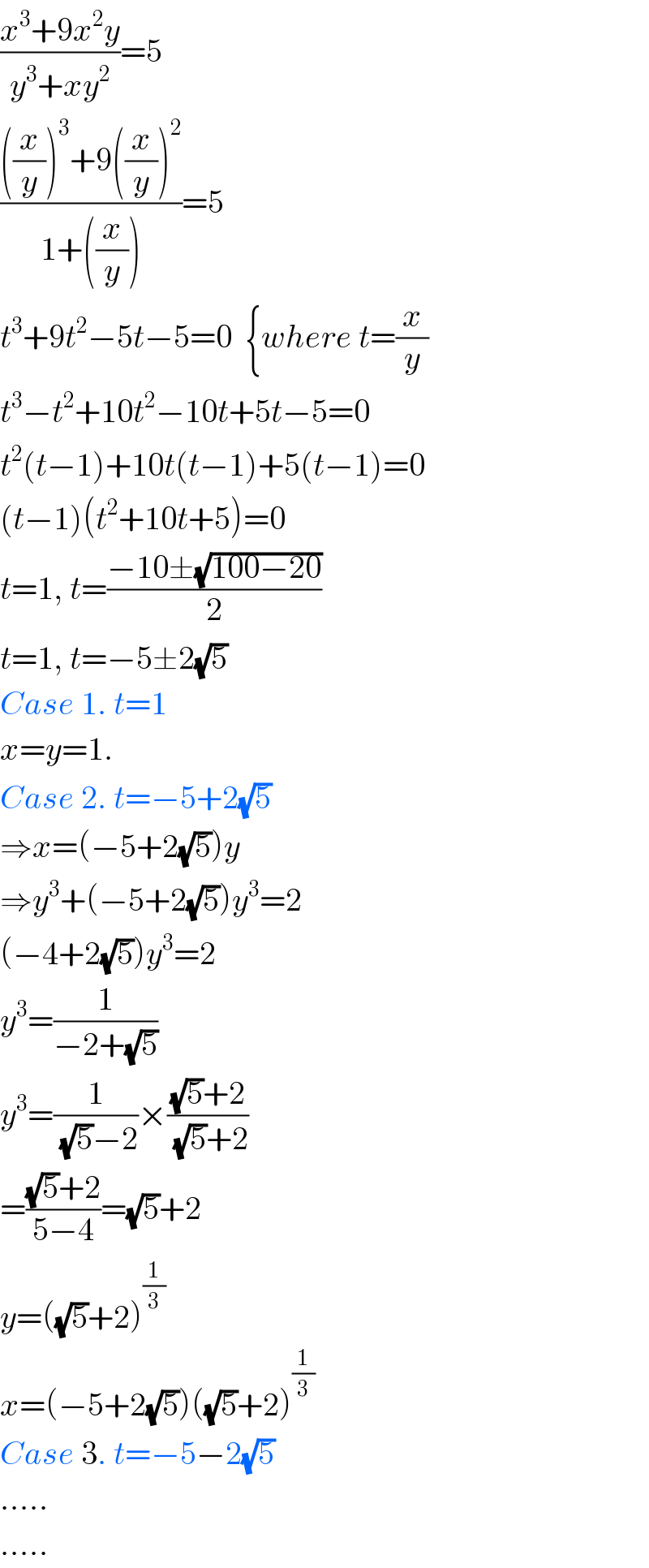
((x^3 +9x^2 y)/(y^3 +xy^2 ))=5 ((((x/y))^3 +9((x/y))^2 )/(1+((x/y))))=5 t^3 +9t^2 −5t−5=0 {where t=(x/y) t^3 −t^2 +10t^2 −10t+5t−5=0 t^2 (t−1)+10t(t−1)+5(t−1)=0 (t−1)(t^2 +10t+5)=0 t=1, t=((−10±(√(100−20)))/2) t=1, t=−5±2(√5) Case 1. t=1 x=y=1. Case 2. t=−5+2(√5) ⇒x=(−5+2(√5))y ⇒y^3 +(−5+2(√5))y^3 =2 (−4+2(√5))y^3 =2 y^3 =(1/(−2+(√5))) y^3 =(1/( (√5)−2))×(((√5)+2)/( (√5)+2)) =(((√5)+2)/(5−4))=(√5)+2 y=((√5)+2)^(1/3) x=(−5+2(√5))((√5)+2)^(1/3) Case 3. t=−5−2(√5) ..... .....
$$\frac{{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} {y}}{{y}^{\mathrm{3}} +{xy}^{\mathrm{2}} }=\mathrm{5} \\ $$$$\frac{\left(\frac{{x}}{{y}}\right)^{\mathrm{3}} +\mathrm{9}\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{x}}{{y}}\right)}=\mathrm{5} \\ $$$${t}^{\mathrm{3}} +\mathrm{9}{t}^{\mathrm{2}} −\mathrm{5}{t}−\mathrm{5}=\mathrm{0}\:\:\left\{{where}\:{t}=\frac{{x}}{{y}}\right. \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{10}{t}^{\mathrm{2}} −\mathrm{10}{t}+\mathrm{5}{t}−\mathrm{5}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)+\mathrm{10}{t}\left({t}−\mathrm{1}\right)+\mathrm{5}\left({t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{10}{t}+\mathrm{5}\right)=\mathrm{0} \\ $$$${t}=\mathrm{1},\:{t}=\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{20}}}{\mathrm{2}} \\ $$$${t}=\mathrm{1},\:{t}=−\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${Case}\:\mathrm{1}.\:{t}=\mathrm{1} \\ $$$${x}={y}=\mathrm{1}. \\ $$$${Case}\:\mathrm{2}.\:{t}=−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{x}=\left(−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right){y} \\ $$$$\Rightarrow{y}^{\mathrm{3}} +\left(−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right){y}^{\mathrm{3}} =\mathrm{2} \\ $$$$\left(−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}}\right){y}^{\mathrm{3}} =\mathrm{2} \\ $$$${y}^{\mathrm{3}} =\frac{\mathrm{1}}{−\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$$${y}^{\mathrm{3}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}×\frac{\sqrt{\mathrm{5}}+\mathrm{2}}{\:\sqrt{\mathrm{5}}+\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{5}}+\mathrm{2}}{\mathrm{5}−\mathrm{4}}=\sqrt{\mathrm{5}}+\mathrm{2} \\ $$$${y}=\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${x}=\left(−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right)\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${Case}\:\mathrm{3}.\:{t}=−\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$….. \\ $$$$….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *