Question Number 92835 by unknown last updated on 09/May/20

Commented by unknown last updated on 09/May/20
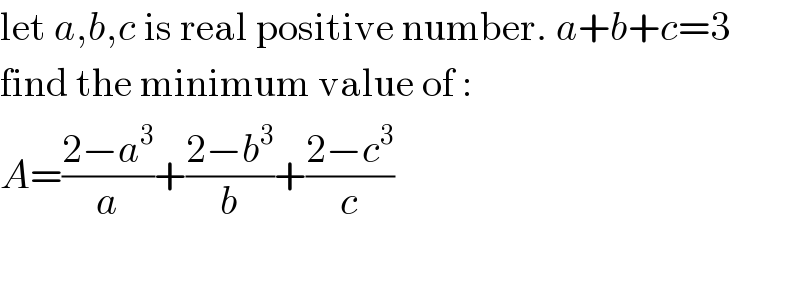
$$\mathrm{let}\:{a},{b},{c}\:\mathrm{is}\:\mathrm{real}\:\mathrm{positive}\:\mathrm{number}.\:{a}+{b}+{c}=\mathrm{3} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:: \\ $$$${A}=\frac{\mathrm{2}−{a}^{\mathrm{3}} }{{a}}+\frac{\mathrm{2}−{b}^{\mathrm{3}} }{{b}}+\frac{\mathrm{2}−{c}^{\mathrm{3}} }{{c}} \\ $$$$ \\ $$
Commented by mr W last updated on 10/May/20
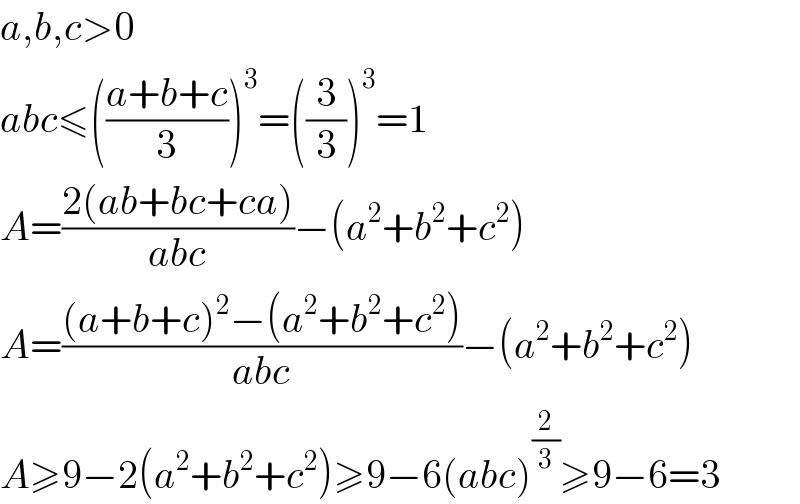
$${a},{b},{c}>\mathrm{0} \\ $$$${abc}\leqslant\left(\frac{{a}+{b}+{c}}{\mathrm{3}}\right)^{\mathrm{3}} =\left(\frac{\mathrm{3}}{\mathrm{3}}\right)^{\mathrm{3}} =\mathrm{1} \\ $$$${A}=\frac{\mathrm{2}\left({ab}+{bc}+{ca}\right)}{{abc}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$${A}=\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{{abc}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$${A}\geqslant\mathrm{9}−\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\geqslant\mathrm{9}−\mathrm{6}\left({abc}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \geqslant\mathrm{9}−\mathrm{6}=\mathrm{3} \\ $$
Commented by unknown last updated on 11/May/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
