Question Number 93031 by Power last updated on 10/May/20
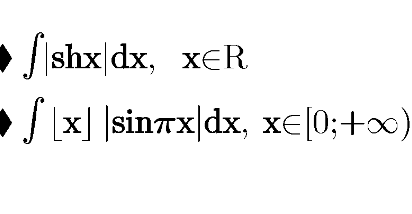
Commented by Power last updated on 10/May/20
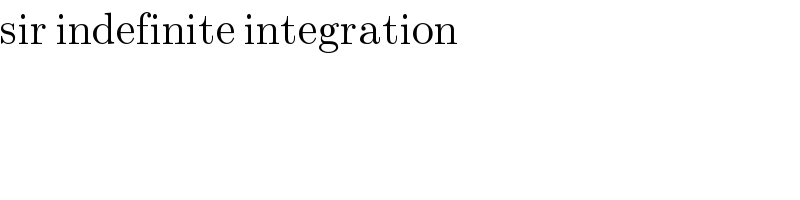
$$\mathrm{sir}\:\mathrm{indefinite}\:\mathrm{integration} \\ $$
Commented by prakash jain last updated on 10/May/20
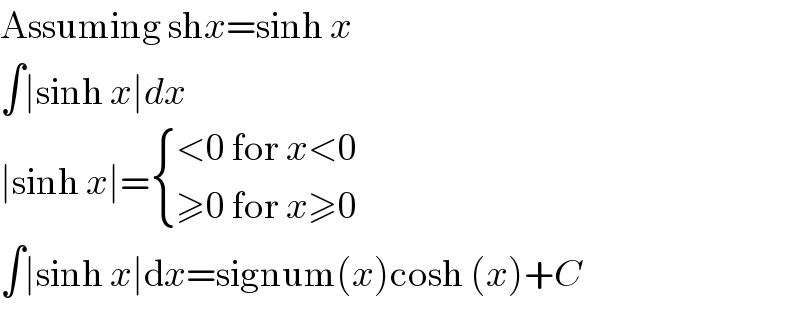
$$\mathrm{Assuming}\:\mathrm{sh}{x}=\mathrm{sinh}\:{x} \\ $$$$\int\mid\mathrm{sinh}\:{x}\mid{dx} \\ $$$$\mid\mathrm{sinh}\:{x}\mid=\begin{cases}{<\mathrm{0}\:\mathrm{for}\:{x}<\mathrm{0}}\\{\geqslant\mathrm{0}\:\mathrm{for}\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$$\int\mid\mathrm{sinh}\:{x}\mid\mathrm{d}{x}=\mathrm{signum}\left({x}\right)\mathrm{cosh}\:\left({x}\right)+{C} \\ $$
Commented by prakash jain last updated on 10/May/20

$$\mathrm{I}\:\mathrm{think}\:\mathrm{indefinite}\:\mathrm{integration}\:\mathrm{is}\: \\ $$$$\mathrm{not}\:\mathrm{possible}\:\mathrm{for}\:\mathrm{functions}\:\mathrm{involving}\:\lfloor{x}\rfloor.\: \\ $$$$\mathrm{I}\:\mathrm{may}\:\mathrm{be}\:\mathrm{wrong}\:\mathrm{though}. \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{find}\:\mathrm{a}\:\mathrm{solution}\:\left(\mathrm{or}\:\mathrm{even}\:\mathrm{just}\:\mathrm{an}\right. \\ $$$$\left.\mathrm{answer}\right),\:\mathrm{please}\:\mathrm{share}. \\ $$
Commented by Power last updated on 10/May/20
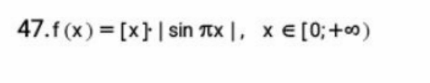
Commented by prakash jain last updated on 10/May/20

$$\mathrm{Which}\:\mathrm{book}? \\ $$
Commented by Power last updated on 10/May/20

$$\mathrm{find}\:\mathrm{the}\:\mathrm{beginning}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{in}\:\mathrm{the}\:\mathrm{book} \\ $$
Commented by Power last updated on 10/May/20

$$\mathrm{from}\:\mathrm{uzbek}\:\mathrm{books} \\ $$
Commented by Power last updated on 10/May/20
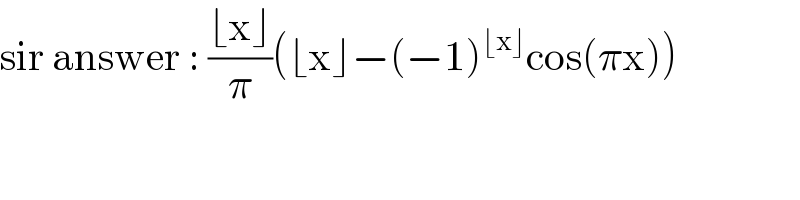
$$\mathrm{sir}\:\mathrm{answer}\::\:\frac{\lfloor\mathrm{x}\rfloor}{\pi}\left(\lfloor\mathrm{x}\rfloor−\left(−\mathrm{1}\right)^{\lfloor\mathrm{x}\rfloor} \mathrm{cos}\left(\pi\mathrm{x}\right)\right) \\ $$
Commented by prakash jain last updated on 10/May/20
Thanks. I will try solving it.
Commented by mathmax by abdo last updated on 10/May/20
![I =∫_0 ^∞ [x] ∣sin(πx)∣ dx ⇒ I =Σ_(n=0) ^∞ ∫_n ^(n+1) n∣sin(πx)∣ dx =Σ_(n=0) ^∞ n A_n with A_n =∫_n ^(n+1) ∣sin(πx)∣dx A_n =_(x=n+t) ∫_0 ^1 ∣sin(π(n+t)∣ dt =∫_0 ^1 ∣sin(πn +πt)∣dt =∫_0 ^1 ∣(−1)^n cos(πt)∣ dt =∫_0 ^1 ∣cos(πt)∣dt =_(πt =u) ∫_0 ^π ∣cos(u)∣(du/π) =(1/π) { ∫_0 ^(π/2) cosu du −∫_(π/2) ^π cosu du} =(1/π){ [sinu]_0 ^(π/2) −[sinu]_(π/2) ^π } =(1/π){ 1−(−1)} =(2/π) ⇒ I =(2/π)Σ_(n=0) ^∞ n =+∞ ⇒I is divergent ...!](https://www.tinkutara.com/question/Q93080.png)
$${I}\:=\int_{\mathrm{0}} ^{\infty} \left[{x}\right]\:\mid{sin}\left(\pi{x}\right)\mid\:{dx}\:\Rightarrow\:{I}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} {n}\mid{sin}\left(\pi{x}\right)\mid\:{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:{n}\:{A}_{{n}} \:\:{with}\:{A}_{{n}} =\int_{{n}} ^{{n}+\mathrm{1}} \mid{sin}\left(\pi{x}\right)\mid{dx} \\ $$$${A}_{{n}} =_{{x}={n}+{t}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mid{sin}\left(\pi\left({n}+{t}\right)\mid\:{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mid{sin}\left(\pi{n}\:+\pi{t}\right)\mid{dt}\right. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mid\left(−\mathrm{1}\right)^{{n}} \:{cos}\left(\pi{t}\right)\mid\:{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mid{cos}\left(\pi{t}\right)\mid{dt} \\ $$$$=_{\pi{t}\:={u}} \:\:\:\int_{\mathrm{0}} ^{\pi} \:\mid{cos}\left({u}\right)\mid\frac{{du}}{\pi}\:=\frac{\mathrm{1}}{\pi}\:\left\{\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosu}\:{du}\:−\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:{cosu}\:{du}\right\} \\ $$$$=\frac{\mathrm{1}}{\pi}\left\{\:\left[{sinu}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:−\left[{sinu}\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\right\}\:=\frac{\mathrm{1}}{\pi}\left\{\:\mathrm{1}−\left(−\mathrm{1}\right)\right\}\:=\frac{\mathrm{2}}{\pi}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{2}}{\pi}\sum_{{n}=\mathrm{0}} ^{\infty} {n}\:=+\infty\:\:\:\Rightarrow{I}\:{is}\:{divergent}\:…! \\ $$
Commented by mathmax by abdo last updated on 10/May/20
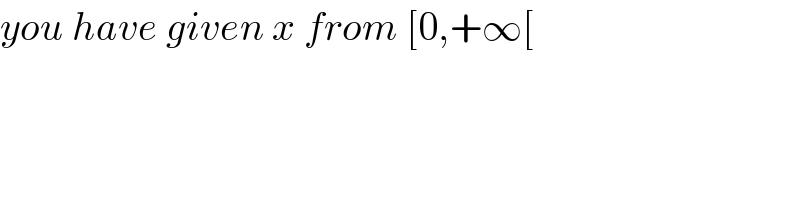
$${you}\:{have}\:{given}\:{x}\:{from}\:\left[\mathrm{0},+\infty\left[\right.\right. \\ $$
Answered by prakash jain last updated on 11/May/20
![f(x)=⌊x⌋∣sin πx∣ f(x)= { (0,(0≤x<1)),((∣sin πx∣),(1≤x<2)),((2∣sinπx∣ ),(2≤x<3)),((n∣sinπx∣ ),(n≤x<(n+1))) :} f(x)=⌊x⌋∣sin πx∣ =⌊x⌋∣sin π(⌊x⌋+{x}) x=⌊x⌋+{x} and sin (nπ+θ)=(−)^n sin θ =⌊x⌋∣(−1)^(⌊x⌋) sin (π{x})∣ =⌊x⌋sin( π{x}) sin π{x}>0 as {x}<1 I=∫f(x)dx=∫_0 ^( x) f(t)dt+C =∫_0 ^1 sin π{t}dt+∫_1 ^2 2sin {πt}dt+..∫_(⌊x⌋) ^x sin (πt)dt sin (πt) is periodic with period 1 =Σ_(n=0) ^(⌊x⌋−1) ∫_0 ^1 sin πtdt+∫_(⌊x⌋) ^x sin πtdt+C =((⌊x⌋(⌊x⌋−1))/2)[−((cos πt)/π)]_0 ^1 +⌊x⌋∫_0 ^({x}) sin πtdt+C =(2/π)×((⌊x⌋(⌊x⌋−1))/2)+⌊x⌋[−((cos πt)/π)]_0 ^({x}) +C =((⌊x⌋(⌊x⌋−1))/π)+((⌊x⌋)/π)(1−cos π{x})+C =((⌊x⌋⌊x⌋)/π)+−((⌊x⌋)/π)cos( π{x})+C =((⌊x⌋⌊x⌋)/π)+−((⌊x⌋)/π)cos( π(x−⌊x⌋)+C =((⌊x⌋⌊x⌋)/π)+−((⌊x⌋)/π)(−1)^(⌊x⌋) cos(πx)+C](https://www.tinkutara.com/question/Q93151.png)
$${f}\left({x}\right)=\lfloor{x}\rfloor\mid\mathrm{sin}\:\pi{x}\mid \\ $$$${f}\left({x}\right)=\begin{cases}{\mathrm{0}}&{\mathrm{0}\leqslant{x}<\mathrm{1}}\\{\mid\mathrm{sin}\:\pi{x}\mid}&{\mathrm{1}\leqslant{x}<\mathrm{2}}\\{\mathrm{2}\mid\mathrm{sin}\pi{x}\mid\:}&{\mathrm{2}\leqslant{x}<\mathrm{3}}\\{{n}\mid\mathrm{sin}\pi{x}\mid\:}&{{n}\leqslant{x}<\left({n}+\mathrm{1}\right)}\end{cases} \\ $$$${f}\left({x}\right)=\lfloor{x}\rfloor\mid\mathrm{sin}\:\pi{x}\mid \\ $$$$=\lfloor{x}\rfloor\mid\mathrm{sin}\:\pi\left(\lfloor{x}\rfloor+\left\{{x}\right\}\right) \\ $$$$\:\:\:\:\:{x}=\lfloor{x}\rfloor+\left\{{x}\right\}\:\:{and}\:\mathrm{sin}\:\left({n}\pi+\theta\right)=\left(−\right)^{{n}} \mathrm{sin}\:\theta \\ $$$$=\lfloor{x}\rfloor\mid\left(−\mathrm{1}\right)^{\lfloor{x}\rfloor} \mathrm{sin}\:\left(\pi\left\{{x}\right\}\right)\mid \\ $$$$=\lfloor{x}\rfloor\mathrm{sin}\left(\:\pi\left\{{x}\right\}\right)\:\:\:\:\mathrm{sin}\:\pi\left\{{x}\right\}>\mathrm{0}\:\mathrm{as}\:\left\{{x}\right\}<\mathrm{1} \\ $$$${I}=\int{f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\:{x}} {f}\left({t}\right){dt}+{C} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}\:\pi\left\{{t}\right\}{dt}+\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{2sin}\:\left\{\pi{t}\right\}{dt}+..\int_{\lfloor{x}\rfloor} ^{{x}} \mathrm{sin}\:\left(\pi{t}\right){dt} \\ $$$$\mathrm{sin}\:\left(\pi{t}\right)\:\mathrm{is}\:\mathrm{periodic}\:\mathrm{with}\:\mathrm{period}\:\mathrm{1} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\lfloor{x}\rfloor−\mathrm{1}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}\:\pi{tdt}+\int_{\lfloor{x}\rfloor} ^{{x}} \mathrm{sin}\:\pi{tdt}+{C} \\ $$$$=\frac{\lfloor{x}\rfloor\left(\lfloor{x}\rfloor−\mathrm{1}\right)}{\mathrm{2}}\left[−\frac{\mathrm{cos}\:\pi{t}}{\pi}\right]_{\mathrm{0}} ^{\mathrm{1}} +\lfloor{x}\rfloor\int_{\mathrm{0}} ^{\left\{{x}\right\}} \mathrm{sin}\:\pi{tdt}+{C} \\ $$$$=\frac{\mathrm{2}}{\pi}×\frac{\lfloor{x}\rfloor\left(\lfloor{x}\rfloor−\mathrm{1}\right)}{\mathrm{2}}+\lfloor{x}\rfloor\left[−\frac{\mathrm{cos}\:\pi{t}}{\pi}\right]_{\mathrm{0}} ^{\left\{{x}\right\}} +{C} \\ $$$$=\frac{\lfloor{x}\rfloor\left(\lfloor{x}\rfloor−\mathrm{1}\right)}{\pi}+\frac{\lfloor{x}\rfloor}{\pi}\left(\mathrm{1}−\mathrm{cos}\:\pi\left\{{x}\right\}\right)+{C} \\ $$$$=\frac{\lfloor{x}\rfloor\lfloor{x}\rfloor}{\pi}+−\frac{\lfloor{x}\rfloor}{\pi}\mathrm{cos}\left(\:\pi\left\{{x}\right\}\right)+{C} \\ $$$$=\frac{\lfloor{x}\rfloor\lfloor{x}\rfloor}{\pi}+−\frac{\lfloor{x}\rfloor}{\pi}\mathrm{cos}\left(\:\pi\left({x}−\lfloor{x}\rfloor\right)+{C}\right. \\ $$$$=\frac{\lfloor{x}\rfloor\lfloor{x}\rfloor}{\pi}+−\frac{\lfloor{x}\rfloor}{\pi}\left(−\mathrm{1}\right)^{\lfloor{x}\rfloor} \mathrm{cos}\left(\pi{x}\right)+{C} \\ $$
Commented by Power last updated on 11/May/20

Commented by Power last updated on 11/May/20

$$\mathrm{thanks} \\ $$
