Question Number 93125 by john santu last updated on 11/May/20
Commented by john santu last updated on 11/May/20
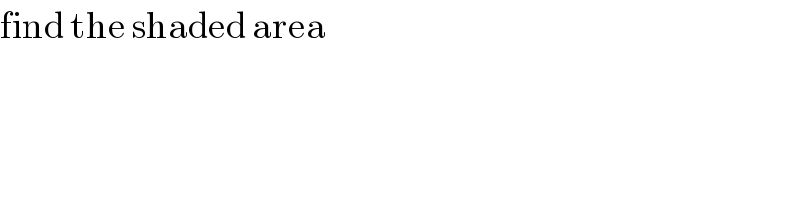
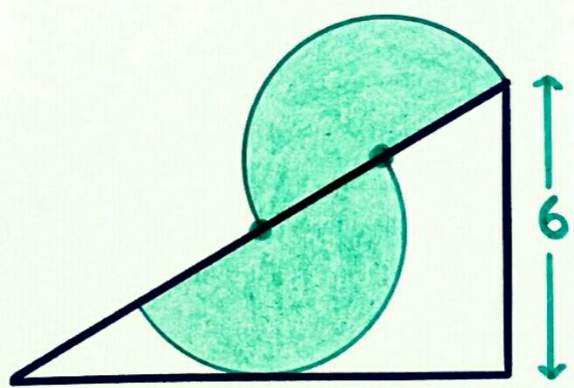
$$\mathrm{find}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{area}\: \\ $$
Commented by i jagooll last updated on 11/May/20
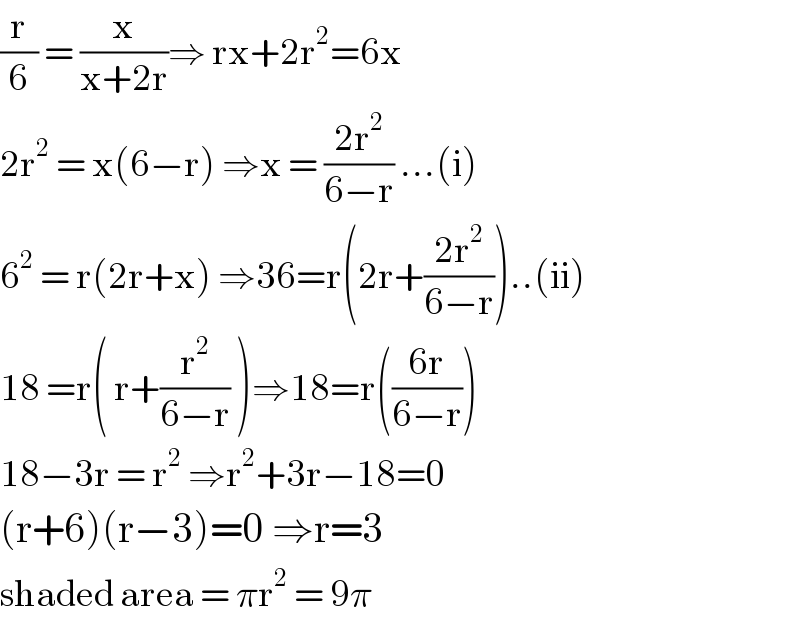
$$\frac{\mathrm{r}}{\mathrm{6}}\:=\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{2r}}\Rightarrow\:\mathrm{rx}+\mathrm{2r}^{\mathrm{2}} =\mathrm{6x} \\ $$$$\mathrm{2r}^{\mathrm{2}} \:=\:\mathrm{x}\left(\mathrm{6}−\mathrm{r}\right)\:\Rightarrow\mathrm{x}\:=\:\frac{\mathrm{2r}^{\mathrm{2}} }{\mathrm{6}−\mathrm{r}}\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{6}^{\mathrm{2}} \:=\:\mathrm{r}\left(\mathrm{2r}+\mathrm{x}\right)\:\Rightarrow\mathrm{36}=\mathrm{r}\left(\mathrm{2r}+\frac{\mathrm{2r}^{\mathrm{2}} }{\mathrm{6}−\mathrm{r}}\right)..\left(\mathrm{ii}\right) \\ $$$$\mathrm{18}\:=\mathrm{r}\left(\:\mathrm{r}+\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{6}−\mathrm{r}}\:\right)\Rightarrow\mathrm{18}=\mathrm{r}\left(\frac{\mathrm{6r}}{\mathrm{6}−\mathrm{r}}\right) \\ $$$$\mathrm{18}−\mathrm{3r}\:=\:\mathrm{r}^{\mathrm{2}} \:\Rightarrow\mathrm{r}^{\mathrm{2}} +\mathrm{3r}−\mathrm{18}=\mathrm{0} \\ $$$$\left(\mathrm{r}+\mathrm{6}\right)\left(\mathrm{r}−\mathrm{3}\right)=\mathrm{0}\:\Rightarrow\mathrm{r}=\mathrm{3} \\ $$$$\mathrm{shaded}\:\mathrm{area}\:=\:\pi\mathrm{r}^{\mathrm{2}} \:=\:\mathrm{9}\pi\: \\ $$
Commented by john santu last updated on 11/May/20
cool man ��������
