Menu Close

Question-93209

Tinku Tara 0 Comments
Pin




Question Number 93209 by Rasheed.Sindhi last updated on 11/May/20
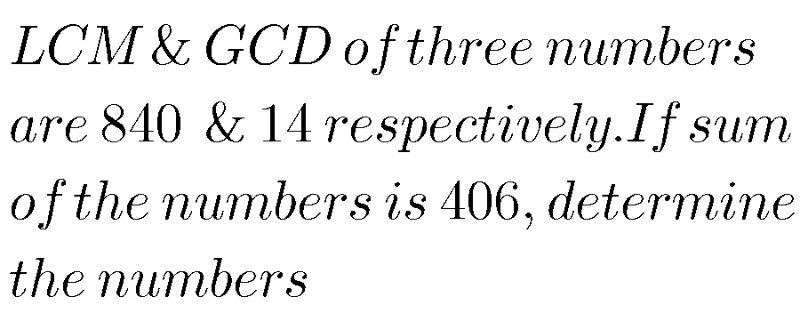
Commented by Rasheed.Sindhi last updated on 12/May/20
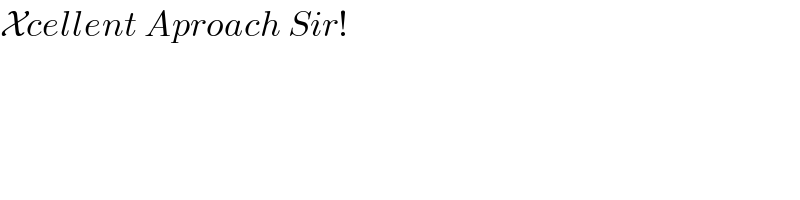
Xcellent Aproach Sir!
$$\mathcal{X}{cellent}\:{Aproach}\:{Sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 12/May/20
Welcome Sir prakash jain! Have seen you in the fotum after long time! You′re one of those from which I′ve learnt a lot!
$${Welcome}\:{Sir}\:{prakash}\:{jain}!\: \\ $$$${Have}\:{seen}\:{you}\:{in}\:{the}\:{fotum}\:{after} \\ $$$${long}\:{time}! \\ $$$${You}'{re}\:{one}\:{of}\:{those}\:{from}\:{which} \\ $$$${I}'{ve}\:{learnt}\:{a}\:{lot}! \\ $$
Commented by prakash jain last updated on 11/May/20
number be 14a,14b,14c a+b+c=29 LCM(a,b,c)=60 Factors of 60 1,2,3,4,5,6,10,12,15,20,30,60 We need to three number such tbat sum a+b+c=29 GCD(a,b,c)=1 20,6,3 20,5,4 15,12,2 15,10,4 numbers are 14a,14b,14c
$$\mathrm{number}\:\mathrm{be}\:\mathrm{14}{a},\mathrm{14}{b},\mathrm{14}{c} \\ $$$${a}+{b}+{c}=\mathrm{29} \\ $$$$\mathrm{LCM}\left({a},{b},{c}\right)=\mathrm{60} \\ $$$$\mathrm{Factors}\:\mathrm{of}\:\mathrm{60} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{10},\mathrm{12},\mathrm{15},\mathrm{20},\mathrm{30},\mathrm{60} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{three}\:\mathrm{number}\:\mathrm{such} \\ $$$$\mathrm{tbat}\:\mathrm{sum}\:{a}+{b}+{c}=\mathrm{29} \\ $$$$\mathrm{GCD}\left({a},{b},{c}\right)=\mathrm{1} \\ $$$$\mathrm{20},\mathrm{6},\mathrm{3}\: \\ $$$$\mathrm{20},\mathrm{5},\mathrm{4} \\ $$$$\mathrm{15},\mathrm{12},\mathrm{2} \\ $$$$\mathrm{15},\mathrm{10},\mathrm{4} \\ $$$$\mathrm{numbers}\:\mathrm{are}\:\mathrm{14}{a},\mathrm{14}{b},\mathrm{14}{c} \\ $$
Commented by prakash jain last updated on 11/May/20
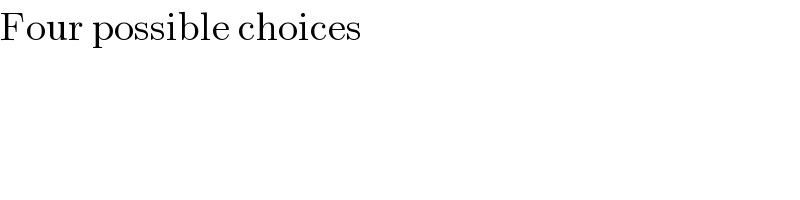
Four possible choices
$$\mathrm{Four}\:\mathrm{possible}\:\mathrm{choices} \\ $$
Commented by prakash jain last updated on 12/May/20
Hi Rasheed, Good to be able to talk to you again. I really miss lot of discussion that we has a few years. I was just now scrolling thru our old discussions in functional equations, number theory and our monthly focus topics. I even found and answer to most recent question in Q119.
$$\mathrm{Hi}\:\mathrm{Rasheed}, \\ $$$$\mathrm{Good}\:\mathrm{to}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{talk}\:\mathrm{to}\:\mathrm{you}\:\mathrm{again}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{miss}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{discussion}\:\mathrm{that}\:\mathrm{we}\:\mathrm{has} \\ $$$$\mathrm{a}\:\mathrm{few}\:\mathrm{years}. \\ $$$$\mathrm{I}\:\mathrm{was}\:\mathrm{just}\:\mathrm{now}\:\mathrm{scrolling}\:\mathrm{thru}\:\mathrm{our} \\ $$$$\mathrm{old}\:\mathrm{discussions}\:\mathrm{in}\:\mathrm{functional} \\ $$$$\mathrm{equations},\:\mathrm{number}\:\mathrm{theory}\:\mathrm{and}\:\mathrm{our} \\ $$$$\mathrm{monthly}\:\mathrm{focus}\:\mathrm{topics}. \\ $$$$\mathrm{I}\:\mathrm{even}\:\mathrm{found}\:\mathrm{and}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{most} \\ $$$$\mathrm{recent}\:\mathrm{question}\:\mathrm{in}\:\mathrm{Q119}. \\ $$
Commented by Rasheed.Sindhi last updated on 12/May/20
Sir, along with you I also remember some other names:Yozii,123456, Mr. flipus and many others and wish that I could contact them!
$${Sir},\:{along}\:{with}\:{you}\:{I}\:{also}\:{remember} \\ $$$${some}\:{other}\:{names}:{Yozii},\mathrm{123456}, \\ $$$${Mr}.\:{flipus}\:{and}\:{many}\:{others}\:{and} \\ $$$${wish}\:{that}\:{I}\:{could}\:{contact}\:{them}! \\ $$
Answered by mr W last updated on 11/May/20
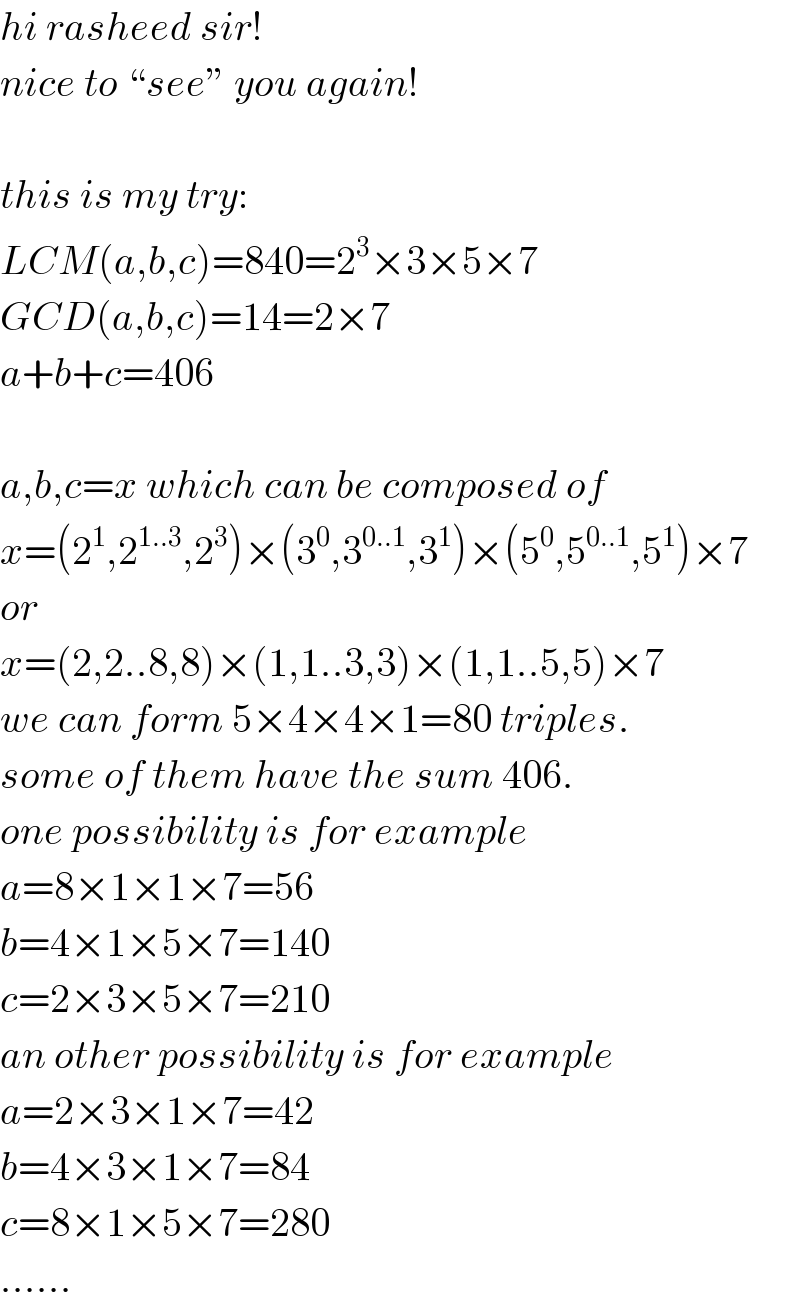
hi rasheed sir! nice to “see” you again! this is my try: LCM(a,b,c)=840=2^3 ×3×5×7 GCD(a,b,c)=14=2×7 a+b+c=406 a,b,c=x which can be composed of x=(2^1 ,2^(1..3) ,2^3 )×(3^0 ,3^(0..1) ,3^1 )×(5^0 ,5^(0..1) ,5^1 )×7 or x=(2,2..8,8)×(1,1..3,3)×(1,1..5,5)×7 we can form 5×4×4×1=80 triples. some of them have the sum 406. one possibility is for example a=8×1×1×7=56 b=4×1×5×7=140 c=2×3×5×7=210 an other possibility is for example a=2×3×1×7=42 b=4×3×1×7=84 c=8×1×5×7=280 ......
$${hi}\:{rasheed}\:{sir}! \\ $$$${nice}\:{to}\:“{see}''\:{you}\:{again}! \\ $$$$ \\ $$$${this}\:{is}\:{my}\:{try}: \\ $$$${LCM}\left({a},{b},{c}\right)=\mathrm{840}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{5}×\mathrm{7} \\ $$$${GCD}\left({a},{b},{c}\right)=\mathrm{14}=\mathrm{2}×\mathrm{7} \\ $$$${a}+{b}+{c}=\mathrm{406} \\ $$$$ \\ $$$${a},{b},{c}={x}\:{which}\:{can}\:{be}\:{composed}\:{of} \\ $$$${x}=\left(\mathrm{2}^{\mathrm{1}} ,\mathrm{2}^{\mathrm{1}..\mathrm{3}} ,\mathrm{2}^{\mathrm{3}} \right)×\left(\mathrm{3}^{\mathrm{0}} ,\mathrm{3}^{\mathrm{0}..\mathrm{1}} ,\mathrm{3}^{\mathrm{1}} \right)×\left(\mathrm{5}^{\mathrm{0}} ,\mathrm{5}^{\mathrm{0}..\mathrm{1}} ,\mathrm{5}^{\mathrm{1}} \right)×\mathrm{7} \\ $$$${or} \\ $$$${x}=\left(\mathrm{2},\mathrm{2}..\mathrm{8},\mathrm{8}\right)×\left(\mathrm{1},\mathrm{1}..\mathrm{3},\mathrm{3}\right)×\left(\mathrm{1},\mathrm{1}..\mathrm{5},\mathrm{5}\right)×\mathrm{7} \\ $$$${we}\:{can}\:{form}\:\mathrm{5}×\mathrm{4}×\mathrm{4}×\mathrm{1}=\mathrm{80}\:{triples}. \\ $$$${some}\:{of}\:{them}\:{have}\:{the}\:{sum}\:\mathrm{406}. \\ $$$${one}\:{possibility}\:{is}\:{for}\:{example} \\ $$$${a}=\mathrm{8}×\mathrm{1}×\mathrm{1}×\mathrm{7}=\mathrm{56} \\ $$$${b}=\mathrm{4}×\mathrm{1}×\mathrm{5}×\mathrm{7}=\mathrm{140} \\ $$$${c}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}=\mathrm{210} \\ $$$${an}\:{other}\:{possibility}\:{is}\:{for}\:{example} \\ $$$${a}=\mathrm{2}×\mathrm{3}×\mathrm{1}×\mathrm{7}=\mathrm{42} \\ $$$${b}=\mathrm{4}×\mathrm{3}×\mathrm{1}×\mathrm{7}=\mathrm{84} \\ $$$${c}=\mathrm{8}×\mathrm{1}×\mathrm{5}×\mathrm{7}=\mathrm{280} \\ $$$$…… \\ $$
Commented by Rasheed.Sindhi last updated on 12/May/20
V. Nice approach Sir!
$$\mathcal{V}.\:\mathcal{N}{ice}\:{approach}\:{Sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 12/May/20
I always be happy to see your posts sir.Although I don′t understand many of them.And really be very happy to know that you also remember me!
$${I}\:{always}\:{be}\:{happy}\:{to}\:{see}\:{your} \\ $$$${posts}\:{sir}.{Although}\:{I}\:{don}'{t}\:{understand} \\ $$$${many}\:{of}\:{them}.{And}\:{really}\:{be}\:{very} \\ $$$${happy}\:{to}\:{know}\:{that}\:{you}\:{also}\:{remember} \\ $$$${me}! \\ $$
Commented by mr W last updated on 12/May/20
thanks sir! certainly i remember you sir. to me you are someone who always tries to solve a question in a way with much and deep thinking, even when it is not always a success. this inspirits very much. somehow i also try to solve a question intensionally in a way which other people may not take. it is not always the best way, but it makes more fun.
$${thanks}\:{sir}!\:{certainly}\:{i}\:{remember}\:{you}\: \\ $$$${sir}.\:{to}\:{me}\:{you}\:{are}\:{someone}\:{who} \\ $$$${always}\:{tries}\:{to}\:{solve}\:{a}\:{question}\:{in}\:{a} \\ $$$${way}\:{with}\:{much}\:{and}\:{deep}\:{thinking}, \\ $$$${even}\:{when}\:{it}\:{is}\:{not}\:{always}\:{a}\:{success}. \\ $$$${this}\:{inspirits}\:{very}\:{much}.\:{somehow} \\ $$$${i}\:{also}\:{try}\:{to}\:{solve}\:{a}\:{question} \\ $$$${intensionally}\:{in}\:{a}\:{way}\:{which}\:{other} \\ $$$${people}\:{may}\:{not}\:{take}.\:{it}\:{is}\:{not}\:{always} \\ $$$${the}\:{best}\:{way},\:{but}\:{it}\:{makes}\:{more}\:{fun}. \\ $$
Commented by Rasheed.Sindhi last updated on 18/May/20
7hank5 sir a └⊚⊤!
$$\mathrm{7}{hank}\mathrm{5}\:{sir}\:\:{a}\:\:\llcorner\circledcirc\top! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *