Question Number 93225 by Ajao yinka last updated on 11/May/20

Commented by prakash jain last updated on 12/May/20
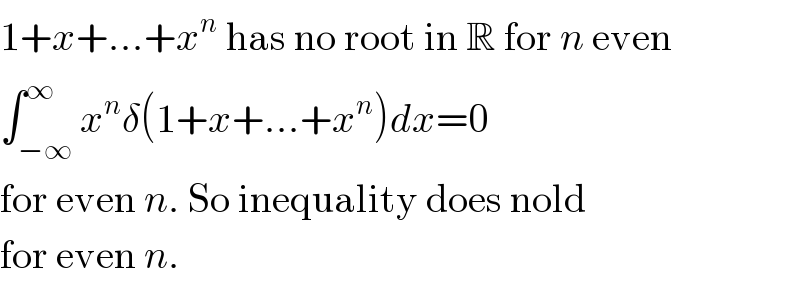
$$\mathrm{1}+{x}+…+{x}^{{n}} \:\mathrm{has}\:\mathrm{no}\:\mathrm{root}\:\mathrm{in}\:\mathbb{R}\:\mathrm{for}\:{n}\:\mathrm{even} \\ $$$$\int_{−\infty} ^{\infty} {x}^{{n}} \delta\left(\mathrm{1}+{x}+…+{x}^{{n}} \right){dx}=\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{even}\:{n}.\:\mathrm{So}\:\mathrm{inequality}\:\mathrm{does}\:\mathrm{nold} \\ $$$$\mathrm{for}\:\mathrm{even}\:{n}. \\ $$
Commented by prakash jain last updated on 12/May/20

$$\mathrm{for}\:{n}\:\mathrm{odd} \\ $$$$\delta\left(\mathrm{1}+{x}+…+{x}^{{n}} \right)=\frac{\delta\left({x}+\mathrm{1}\right)}{\mid\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +..+{nx}^{{n}−\mathrm{1}} \mid_{{x}=−\mathrm{1}} } \\ $$$$\mathrm{S}=\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +…+{nx}^{{n}−\mathrm{1}} \\ $$$${xS}=\:\:\:\:\:\:{x}+\mathrm{2}{x}^{\mathrm{2}} +….+\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{1}} +{nx}^{{n}} \\ $$$$\left(\mathrm{1}−{x}\right){S}=\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +..+{x}^{{n}−\mathrm{1}} \right)−{nx}^{{n}} \\ $$$${x}=−\mathrm{1} \\ $$$$\mathrm{2}{S}={n}+\mathrm{1}\:\left({n}\:{odd}\right) \\ $$$${S}=\frac{{n}+\mathrm{1}}{\mathrm{2}} \\ $$$$\delta\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +..+{x}^{{n}} \right)=\frac{\mathrm{2}\delta\left({x}+\mathrm{1}\right)}{{n}+\mathrm{1}}\:\left({n}\:{odd}\right) \\ $$$$\mathrm{So}\:\mathrm{for}\:\mathrm{odd}\:{n} \\ $$$$\int_{−\infty} ^{+\infty} {x}^{{n}+\mathrm{1}} \delta\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…+{x}^{{n}} \right){dx}=\frac{\mathrm{2}}{{n}+\mathrm{1}} \\ $$
