Menu Close

Question-93439

Tinku Tara 0 Comments
Pin




Question Number 93439 by i jagooll last updated on 13/May/20
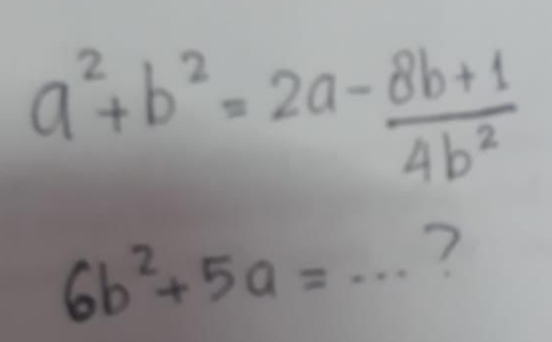
Answered by niroj last updated on 13/May/20
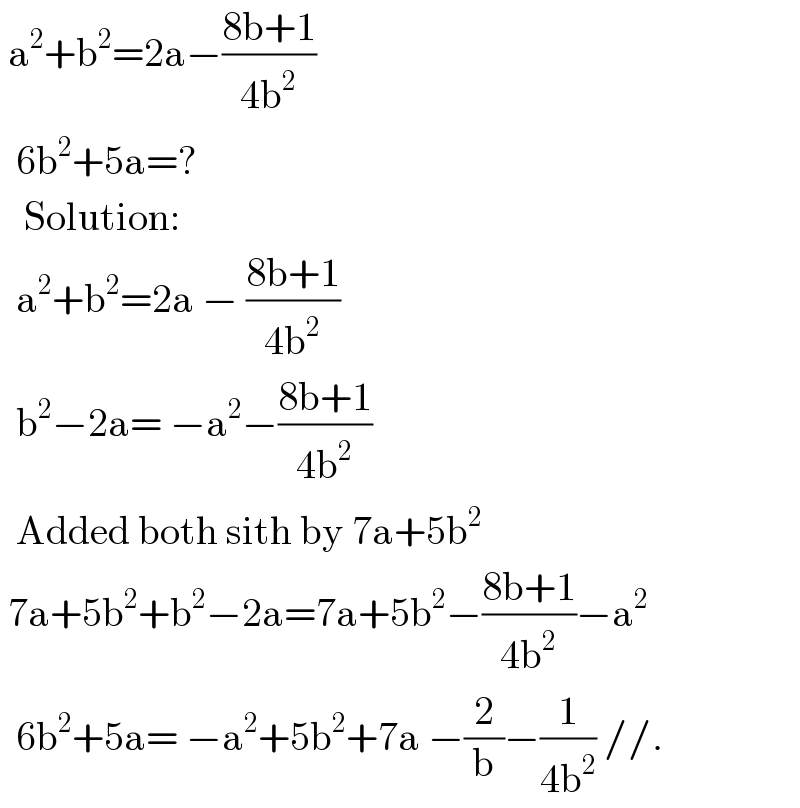
a^2 +b^2 =2a−((8b+1)/(4b^2 )) 6b^2 +5a=? Solution: a^2 +b^2 =2a − ((8b+1)/(4b^2 )) b^2 −2a= −a^2 −((8b+1)/(4b^2 )) Added both sith by 7a+5b^2 7a+5b^2 +b^2 −2a=7a+5b^2 −((8b+1)/(4b^2 ))−a^2 6b^2 +5a= −a^2 +5b^2 +7a −(2/b)−(1/(4b^2 )) //.
$$\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{2a}−\frac{\mathrm{8b}+\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} } \\ $$$$\:\:\mathrm{6b}^{\mathrm{2}} +\mathrm{5a}=? \\ $$$$\:\:\:\mathrm{Solution}: \\ $$$$\:\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{2a}\:−\:\frac{\mathrm{8b}+\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} } \\ $$$$\:\:\mathrm{b}^{\mathrm{2}} −\mathrm{2a}=\:−\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{8b}+\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} } \\ $$$$\:\:\mathrm{Added}\:\mathrm{both}\:\mathrm{sith}\:\mathrm{by}\:\mathrm{7a}+\mathrm{5b}^{\mathrm{2}} \\ $$$$\:\mathrm{7a}+\mathrm{5b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2a}=\mathrm{7a}+\mathrm{5b}^{\mathrm{2}} −\frac{\mathrm{8b}+\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} }−\mathrm{a}^{\mathrm{2}} \\ $$$$\:\:\mathrm{6b}^{\mathrm{2}} +\mathrm{5a}=\:−\mathrm{a}^{\mathrm{2}} +\mathrm{5b}^{\mathrm{2}} +\mathrm{7a}\:−\frac{\mathrm{2}}{\mathrm{b}}−\frac{\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} }\://. \\ $$
Commented by i jagooll last updated on 13/May/20
but the answer is in number sir
Commented by niroj last updated on 13/May/20
According your que^n it comes if want in numerical answer Pls make sure que^n is clear my dear.
$${According}\:{your}\:{que}^{{n}} \:{it}\:{comes} \\ $$$$\:{if}\:\:{want}\:{in}\:{numerical}\:{answer} \\ $$$${Pls}\:{make}\:{sure}\:{que}^{{n}} \:{is}\:{clear}\:{my}\:{dear}. \\ $$
Commented by i jagooll last updated on 13/May/20
yes sir. written in the book so the problem
Answered by 1549442205 last updated on 13/May/20
I think that this problem has not numberal result .Inddeed,it is easy to see that a=((1±(√(−(2b^2 −1)^2 −8b)))/(2b)) (we consider as a quadratic equation of a).Hence 6b^2 +5a can receive a lot of different values .We only need a condition that (2b^2 −1)^2 +8b)≤0(for △≥0)
$$\mathrm{I}\:\mathrm{think}\:\:\mathrm{that}\:\mathrm{this}\:\mathrm{problem}\:\mathrm{has}\:\mathrm{not}\:\mathrm{numberal} \\ $$$$\mathrm{result}\:.\mathrm{Inddeed},\mathrm{it}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\: \\ $$$$\mathrm{a}=\frac{\mathrm{1}\pm\sqrt{−\left(\mathrm{2b}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{8b}}}{\mathrm{2b}}\:\left(\mathrm{we}\:\mathrm{consider}\:\mathrm{as}\:\mathrm{a}\:\right. \\ $$$$\left.\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\right).\mathrm{Hence}\:\mathrm{6b}^{\mathrm{2}} +\mathrm{5a}\:\mathrm{can} \\ $$$$\mathrm{receive}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{different}\:\mathrm{values}\:.\mathrm{We}\:\mathrm{only}\:\mathrm{need} \\ $$$$\left.\mathrm{a}\:\mathrm{condition}\:\mathrm{that}\:\left(\mathrm{2b}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8b}\right)\leqslant\mathrm{0}\left(\mathrm{for}\:\bigtriangleup\geqslant\mathrm{0}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *