Menu Close

Question-93626

Tinku Tara 0 Comments
Pin




Question Number 93626 by i jagooll last updated on 14/May/20
Commented by MJS last updated on 14/May/20
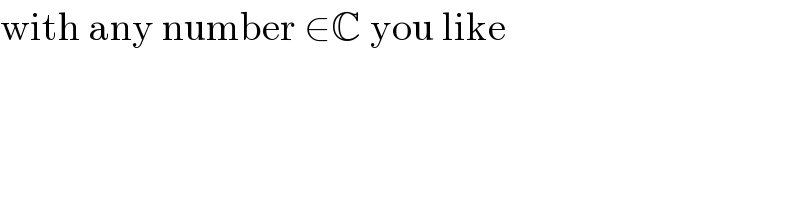
with any number ∈C you like
$$\mathrm{with}\:\mathrm{any}\:\mathrm{number}\:\in\mathbb{C}\:\mathrm{you}\:\mathrm{like} \\ $$
Commented by john santu last updated on 14/May/20
real number sir
$$\mathrm{real}\:\mathrm{number}\:\mathrm{sir} \\ $$
Commented by i jagooll last updated on 14/May/20
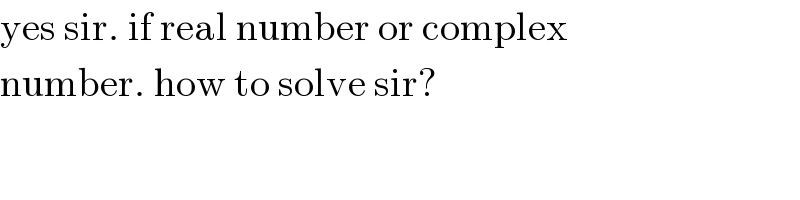
yes sir. if real number or complex number. how to solve sir?
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{if}\:\mathrm{real}\:\mathrm{number}\:\mathrm{or}\:\mathrm{complex} \\ $$$$\mathrm{number}.\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{sir}? \\ $$
Commented by MJS last updated on 14/May/20
x∈C is possible ⇒ x∈R is also possible what are we allowed to do? there′s a unique polynome of 6^(th) degree f(x)=Σ_(j=0) ^6 c_j x^j with f(1)=9, f(2)=18, ... f(7)=104 but if we are free to use any model, why not use g(x)=Σ_(j=0) ^6 (c_j /x^j ) ? this also leads to an unique solution. or use any of the zillions of possibilities or just insert your birth date. we can find a function h(x) with h(8)=(π^e /γ) ...
$${x}\in\mathbb{C}\:\mathrm{is}\:\mathrm{possible}\:\Rightarrow\:{x}\in\mathbb{R}\:\mathrm{is}\:\mathrm{also}\:\mathrm{possible} \\ $$$$ \\ $$$$\mathrm{what}\:\mathrm{are}\:\mathrm{we}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{do}? \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{unique}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{degree} \\ $$$${f}\left({x}\right)=\underset{{j}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}{c}_{{j}} {x}^{{j}} \:\:\mathrm{with}\:{f}\left(\mathrm{1}\right)=\mathrm{9},\:{f}\left(\mathrm{2}\right)=\mathrm{18},\:…\:{f}\left(\mathrm{7}\right)=\mathrm{104} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{are}\:\mathrm{free}\:\mathrm{to}\:\mathrm{use}\:\mathrm{any}\:\mathrm{model},\:\mathrm{why}\:\mathrm{not} \\ $$$$\mathrm{use}\:{g}\left({x}\right)=\underset{{j}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\frac{{c}_{{j}} }{{x}^{{j}} }\:?\:\mathrm{this}\:\mathrm{also}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{an}\:\mathrm{unique} \\ $$$$\mathrm{solution}.\:\mathrm{or}\:\mathrm{use}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the}\:\mathrm{zillions}\:\mathrm{of}\:\mathrm{possibilities} \\ $$$$ \\ $$$$\mathrm{or}\:\mathrm{just}\:\mathrm{insert}\:\mathrm{your}\:\mathrm{birth}\:\mathrm{date}.\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{a} \\ $$$$\mathrm{function}\:{h}\left({x}\right)\:\mathrm{with}\:{h}\left(\mathrm{8}\right)=\frac{\pi^{\mathrm{e}} }{\gamma}\:… \\ $$
Commented by prakash jain last updated on 14/May/20
Given any finite sequence there infinite number of formulas for a_n which sstify the finite terms.
$$\mathrm{Given}\:\mathrm{any}\:\mathrm{finite}\:\mathrm{sequence}\:\mathrm{there} \\ $$$$\mathrm{infinite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{formulas}\:\mathrm{for}\:{a}_{{n}} \\ $$$$\mathrm{which}\:\mathrm{sstify}\:\mathrm{the}\:\mathrm{finite}\:\mathrm{terms}. \\ $$
Commented by i jagooll last updated on 14/May/20
hahaha...����
Commented by prakash jain last updated on 14/May/20
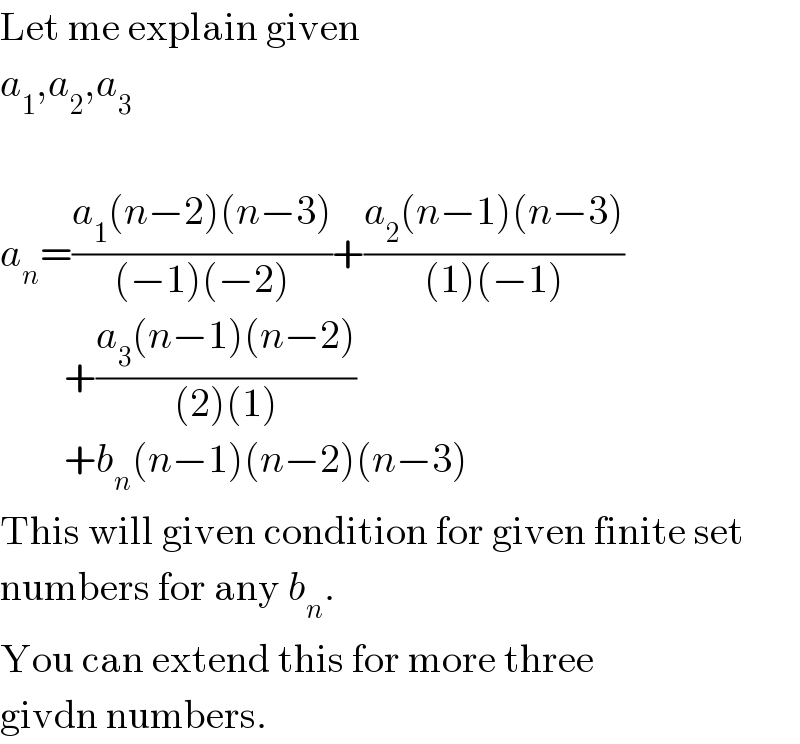
Let me explain given a_1 ,a_2 ,a_3 a_n =((a_1 (n−2)(n−3))/((−1)(−2)))+((a_2 (n−1)(n−3))/((1)(−1))) +((a_3 (n−1)(n−2))/((2)(1))) +b_n (n−1)(n−2)(n−3) This will given condition for given finite set numbers for any b_n . You can extend this for more three givdn numbers.
$$\mathrm{Let}\:\mathrm{me}\:\mathrm{explain}\:\mathrm{given} \\ $$$${a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{a}_{\mathrm{3}} \\ $$$$ \\ $$$${a}_{{n}} =\frac{{a}_{\mathrm{1}} \left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)}{\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)}+\frac{{a}_{\mathrm{2}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{3}\right)}{\left(\mathrm{1}\right)\left(−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:+\frac{{a}_{\mathrm{3}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\left(\mathrm{2}\right)\left(\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:+{b}_{{n}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right) \\ $$$$\mathrm{This}\:\mathrm{will}\:\mathrm{given}\:\mathrm{condition}\:\mathrm{for}\:\mathrm{given}\:\mathrm{finite}\:\mathrm{set} \\ $$$$\mathrm{numbers}\:\mathrm{for}\:\mathrm{any}\:{b}_{{n}} . \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{extend}\:\mathrm{this}\:\mathrm{for}\:\mathrm{more}\:\mathrm{three} \\ $$$$\mathrm{givdn}\:\mathrm{numbers}. \\ $$
Commented by prakash jain last updated on 14/May/20
I hope you get general idea about why answers are not unique.
Commented by i jagooll last updated on 14/May/20
thank you sir. i can try
Answered by MJS last updated on 14/May/20
if it′s a polynome calculate the differences and continue until all numbers in a line are equal. then go back 9 18 20 61 63 79 104 −558 9 2 41 2 16 25 −662 −7 39 −39 14 9 −687 46 −78 53 −5 −696 −124 131 −58 −691 255 −189 −633 −444
$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{differences} \\ $$$$\mathrm{and}\:\mathrm{continue}\:\mathrm{until}\:\mathrm{all}\:\mathrm{numbers}\:\mathrm{in}\:\mathrm{a}\:\mathrm{line}\:\mathrm{are} \\ $$$$\mathrm{equal}.\:\mathrm{then}\:\mathrm{go}\:\mathrm{back} \\ $$$$\mathrm{9}\:\:\mathrm{18}\:\:\mathrm{20}\:\:\mathrm{61}\:\:\mathrm{63}\:\:\mathrm{79}\:\:\mathrm{104}\:\:−\mathrm{558} \\ $$$$\mathrm{9}\:\:\mathrm{2}\:\:\mathrm{41}\:\:\mathrm{2}\:\:\mathrm{16}\:\:\mathrm{25}\:\:−\mathrm{662} \\ $$$$−\mathrm{7}\:\:\mathrm{39}\:\:−\mathrm{39}\:\:\mathrm{14}\:\:\mathrm{9}\:\:−\mathrm{687} \\ $$$$\mathrm{46}\:\:−\mathrm{78}\:\:\mathrm{53}\:\:−\mathrm{5}\:\:−\mathrm{696} \\ $$$$−\mathrm{124}\:\:\mathrm{131}\:\:−\mathrm{58}\:\:−\mathrm{691} \\ $$$$\mathrm{255}\:\:−\mathrm{189}\:\:−\mathrm{633} \\ $$$$−\mathrm{444} \\ $$
Commented by i jagooll last updated on 14/May/20
thanks sir.
$$\mathrm{thanks}\:\mathrm{sir}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *