Question Number 93787 by Ar Brandon last updated on 14/May/20

Commented by mathmax by abdo last updated on 15/May/20

$$\frac{\mathrm{4}{k}}{\mathrm{4}{k}^{\mathrm{4}} \:+\mathrm{1}}\:=\frac{\mathrm{4}{k}}{\left(\sqrt{\mathrm{2}}{k}\right)^{\mathrm{4}} +\mathrm{1}}\:=\frac{\mathrm{4}{k}}{\left(\left(\sqrt{\mathrm{2}}{k}\right)^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{4}{k}}{\left(\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{k}^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{4}{k}}{\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{k}\right)\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{k}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2}{k}\right)}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{2}{k}} \\ $$$$\Rightarrow\:{A}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$${let}\:{u}_{{k}} =\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{2}{k}\:+\mathrm{1}\:\Rightarrow{u}_{{k}−\mathrm{1}} =\mathrm{2}\left({k}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left({k}−\mathrm{1}\right)+\mathrm{1} \\ $$$$=\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}\right)+\mathrm{2}{k}−\mathrm{2}\:+\mathrm{1}\:=\mathrm{2}{k}^{\mathrm{2}} −\mathrm{4}{k}\:+\mathrm{2}\:+\mathrm{2}{k}−\mathrm{1} \\ $$$$=\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}\:+\mathrm{1}\:\Rightarrow\:{A}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{u}_{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{{u}_{{n}} }\right) \\ $$$${A}_{{n}} \:=\frac{\mathrm{1}}{{u}_{\mathrm{0}} }−\frac{\mathrm{1}}{{u}_{\mathrm{1}} }\:+\frac{\mathrm{1}}{{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{{u}_{\mathrm{2}} }\:+….+\frac{\mathrm{1}}{{u}_{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{{u}_{{n}} }\:=\frac{\mathrm{1}}{{u}_{\mathrm{0}} }−\frac{\mathrm{1}}{{u}_{{n}} } \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}}\:=\frac{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}−\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}}\:=\frac{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}}{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Rightarrow\:{A}_{{n}} =\frac{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}}{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}}\:\:{and}\:{we}\:{see}\:{that}\:{lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 15/May/20
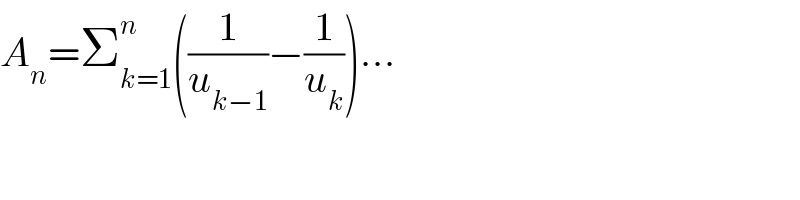
$${A}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{u}_{{k}−\mathrm{1}} }−\frac{\mathrm{1}}{{u}_{{k}} }\right)… \\ $$
Commented by Ar Brandon last updated on 15/May/20
Great ��
Commented by mathmax by abdo last updated on 15/May/20

$${thanks} \\ $$
