Question-93976

Question Number 93976 by i jagooll last updated on 16/May/20

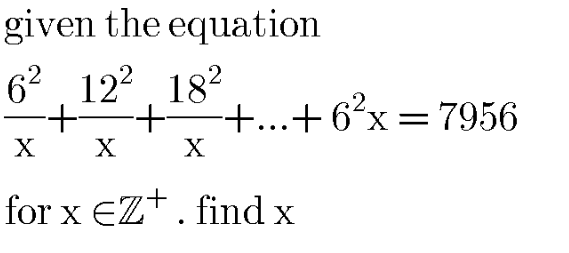
Commented by i jagooll last updated on 16/May/20

can anyone help me ?

Commented by i jagooll last updated on 16/May/20

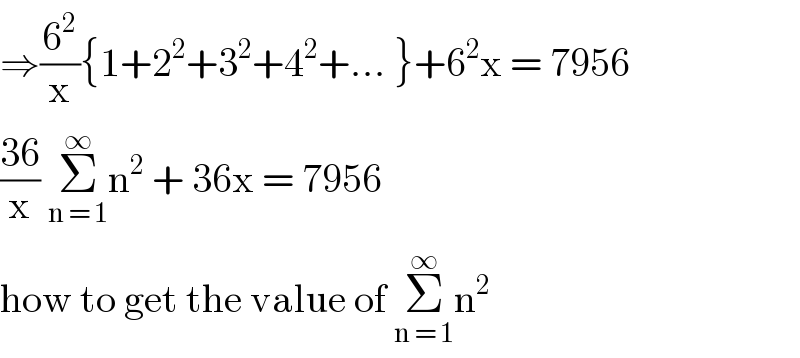
$$\Rightarrow\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{x}}\left\{\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +…\:\right\}+\mathrm{6}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{7956} \\ $$$$\frac{\mathrm{36}}{\mathrm{x}}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}^{\mathrm{2}} \:+\:\mathrm{36x}\:=\:\mathrm{7956} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}^{\mathrm{2}} \\ $$

Commented by i jagooll last updated on 16/May/20

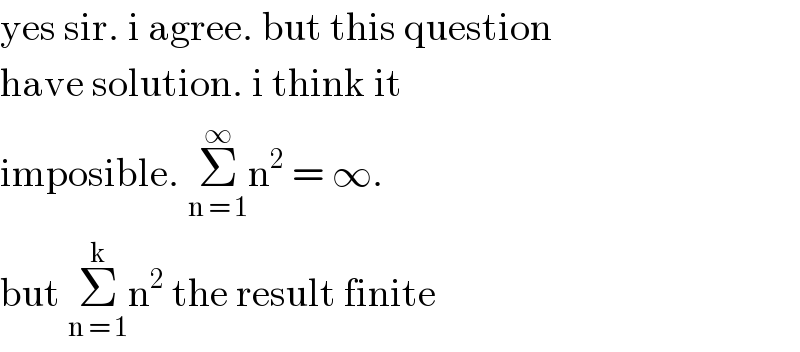
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{agree}.\:\mathrm{but}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{have}\:\mathrm{solution}.\:\mathrm{i}\:\mathrm{think}\:\mathrm{it}\: \\ $$$$\mathrm{imposible}.\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}^{\mathrm{2}} \:=\:\infty. \\ $$$$\mathrm{but}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{n}^{\mathrm{2}} \:\mathrm{the}\:\mathrm{result}\:\mathrm{finite} \\ $$

Commented by PRITHWISH SEN 2 last updated on 16/May/20

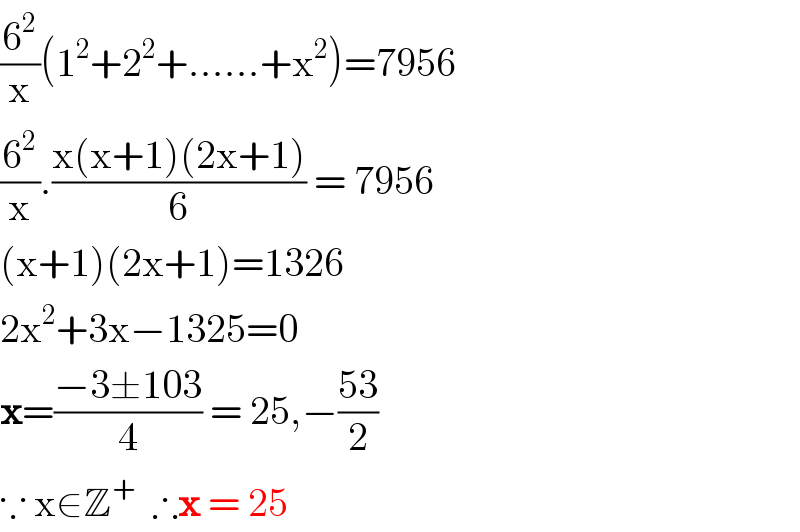
$$\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{x}}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +……+\mathrm{x}^{\mathrm{2}} \right)=\mathrm{7956} \\ $$$$\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{x}}.\frac{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{1}\right)}{\mathrm{6}}\:=\:\mathrm{7956} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{1326} \\ $$$$\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{1325}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{x}}=\frac{−\mathrm{3}\pm\mathrm{103}}{\mathrm{4}}\:=\:\mathrm{25},−\frac{\mathrm{53}}{\mathrm{2}} \\ $$$$\because\:\mathrm{x}\in\mathbb{Z}^{+} \:\:\therefore\boldsymbol{\mathrm{x}}\:=\:\mathrm{25} \\ $$

Commented by mr W last updated on 16/May/20

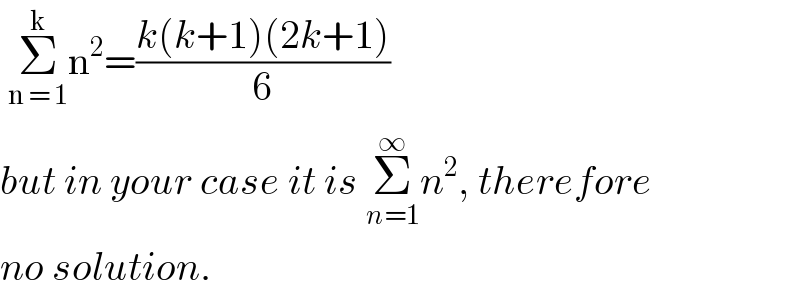
$$\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{n}^{\mathrm{2}} =\frac{{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$${but}\:{in}\:{your}\:{case}\:{it}\:{is}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} ,\:{therefore} \\ $$$${no}\:{solution}. \\ $$

Commented by mr W last updated on 16/May/20

$${no}\:{solution}! \\ $$$${LHS}\rightarrow\infty \\ $$

Commented by mr W last updated on 16/May/20

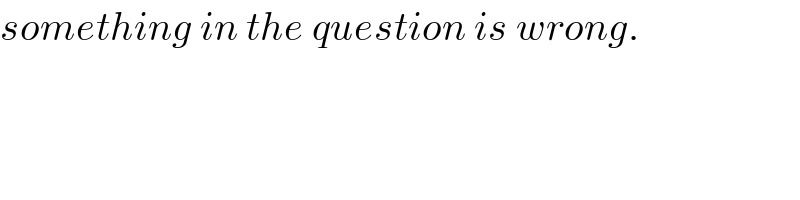
$${something}\:{in}\:{the}\:{question}\:{is}\:{wrong}. \\ $$

Commented by i jagooll last updated on 16/May/20

$$\mathrm{oo}\:\mathrm{maybe}\:\mathrm{the}\:\mathrm{purpose}\:\mathrm{is}\:\mathrm{like} \\ $$$$\mathrm{that},\:\mathrm{a}\:\mathrm{little}\:\mathrm{ambiguos}\:\mathrm{writing} \\ $$

Commented by Kunal12588 last updated on 16/May/20

Yeah sometimes question are written in wrong manners. Once in one my exam a question was to differentiate sinx³. It clearly seems we have to diffrentiate sin(x^3). But my techer said it was sin³ x, when I complained for my marks. And the most wrong thing is every student in my class was able to do that because it was also in our book with same formatting.

Commented by i jagooll last updated on 16/May/20

correctly. I agree

Answered by Kunal12588 last updated on 16/May/20

$$\frac{\mathrm{6}^{\mathrm{2}} }{{x}}\left[\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +.\mathrm{3}^{\mathrm{2}} +…+{x}^{\mathrm{2}} \right]=\mathrm{7956} \\ $$$$\Rightarrow\frac{\mathrm{6}^{\mathrm{2}} }{{x}}×\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}=\mathrm{7956} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)=\mathrm{1326} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1325}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}+\mathrm{4}×\mathrm{2}×\mathrm{1325}}}{\mathrm{4}} \\ $$$${x}=\mathrm{25}\left[{positive}\:{value}\right] \\ $$

Commented by i jagooll last updated on 16/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com