Question Number 93986 by $@ty@m123 last updated on 16/May/20

Answered by mr W last updated on 16/May/20
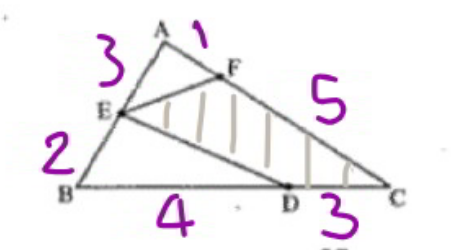
Commented by mr W last updated on 16/May/20
![[AEF]=(3/5)[ABF]=(3/5)×(1/6)[ABC] [BED]=(2/5)[BAD]=(2/5)×(4/7)[ABC] [EFCD]=[ABC]−[AEF]−[BED] =(1−(3/5)×(1/6)−(2/5)×(4/7))[ABC] =((47)/(70))[ABC] ⇒(([EFCD])/([ABC]))=((47)/(70))](https://www.tinkutara.com/question/Q94112.png)
$$\left[{AEF}\right]=\frac{\mathrm{3}}{\mathrm{5}}\left[{ABF}\right]=\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{6}}\left[{ABC}\right] \\ $$$$\left[{BED}\right]=\frac{\mathrm{2}}{\mathrm{5}}\left[{BAD}\right]=\frac{\mathrm{2}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{7}}\left[{ABC}\right] \\ $$$$\left[{EFCD}\right]=\left[{ABC}\right]−\left[{AEF}\right]−\left[{BED}\right] \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{2}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{7}}\right)\left[{ABC}\right] \\ $$$$=\frac{\mathrm{47}}{\mathrm{70}}\left[{ABC}\right] \\ $$$$\Rightarrow\frac{\left[{EFCD}\right]}{\left[{ABC}\right]}=\frac{\mathrm{47}}{\mathrm{70}} \\ $$
Commented by $@ty@m123 last updated on 17/May/20

$${Thanks}\:{a}\:{lot}. \\ $$
Answered by $@ty@m123 last updated on 17/May/20

Commented by $@ty@m123 last updated on 17/May/20
Got an alternative solution from my friend.
