Menu Close

Question-94110

Tinku Tara 0 Comments
Pin




Question Number 94110 by Jidda28 last updated on 16/May/20
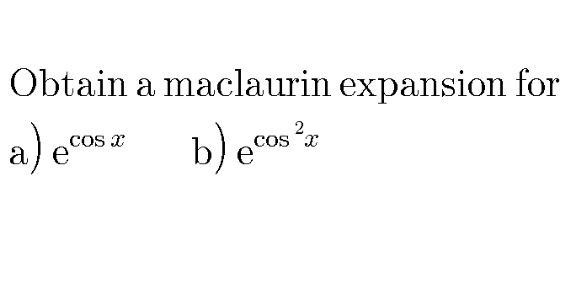
Commented by mathmax by abdo last updated on 17/May/20
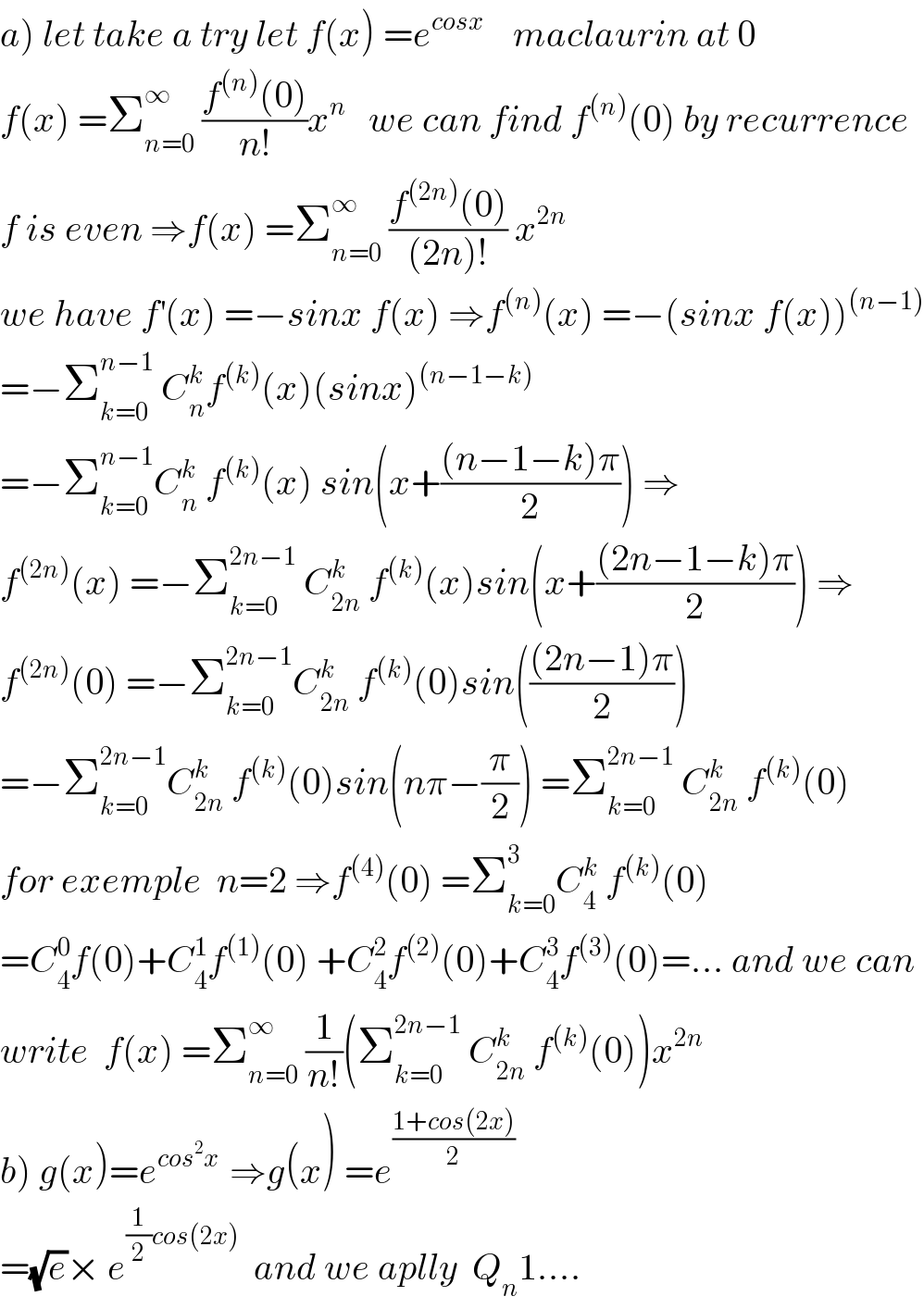
a) let take a try let f(x) =e^(cosx) maclaurin at 0 f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!))x^n we can find f^((n)) (0) by recurrence f is even ⇒f(x) =Σ_(n=0) ^∞ ((f^((2n)) (0))/((2n)!)) x^(2n) we have f^′ (x) =−sinx f(x) ⇒f^((n)) (x) =−(sinx f(x))^((n−1)) =−Σ_(k=0) ^(n−1) C_n ^k f^((k)) (x)(sinx)^((n−1−k)) =−Σ_(k=0) ^(n−1) C_n ^k f^((k)) (x) sin(x+(((n−1−k)π)/2)) ⇒ f^((2n)) (x) =−Σ_(k=0) ^(2n−1) C_(2n) ^k f^((k)) (x)sin(x+(((2n−1−k)π)/2)) ⇒ f^((2n)) (0) =−Σ_(k=0) ^(2n−1) C_(2n) ^k f^((k)) (0)sin((((2n−1)π)/2)) =−Σ_(k=0) ^(2n−1) C_(2n) ^k f^((k)) (0)sin(nπ−(π/2)) =Σ_(k=0) ^(2n−1) C_(2n) ^k f^((k)) (0) for exemple n=2 ⇒f^((4)) (0) =Σ_(k=0) ^3 C_4 ^k f^((k)) (0) =C_4 ^0 f(0)+C_4 ^1 f^((1)) (0) +C_4 ^2 f^((2)) (0)+C_4 ^3 f^((3)) (0)=... and we can write f(x) =Σ_(n=0) ^∞ (1/(n!))(Σ_(k=0) ^(2n−1) C_(2n) ^k f^((k)) (0))x^(2n) b) g(x)=e^(cos^2 x ) ⇒g(x) =e^((1+cos(2x))/2) =(√e)× e^((1/2)cos(2x)) and we aplly Q_n 1....
$$\left.{a}\right)\:{let}\:{take}\:{a}\:{try}\:{let}\:{f}\left({x}\right)\:={e}^{{cosx}} \:\:\:\:{maclaurin}\:{at}\:\mathrm{0} \\ $$$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \:\:\:{we}\:{can}\:{find}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:{by}\:{recurrence} \\ $$$${f}\:{is}\:{even}\:\Rightarrow{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left(\mathrm{2}{n}\right)} \left(\mathrm{0}\right)}{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}} \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)\:=−{sinx}\:{f}\left({x}\right)\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)\:=−\left({sinx}\:{f}\left({x}\right)\right)^{\left({n}−\mathrm{1}\right)} \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{k}} {f}^{\left({k}\right)} \left({x}\right)\left({sinx}\right)^{\left({n}−\mathrm{1}−{k}\right)} \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {C}_{{n}} ^{{k}} \:{f}^{\left({k}\right)} \left({x}\right)\:{sin}\left({x}+\frac{\left({n}−\mathrm{1}−{k}\right)\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{2}{n}\right)} \left({x}\right)\:=−\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:{f}^{\left({k}\right)} \left({x}\right){sin}\left({x}+\frac{\left(\mathrm{2}{n}−\mathrm{1}−{k}\right)\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{2}{n}\right)} \left(\mathrm{0}\right)\:=−\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} {C}_{\mathrm{2}{n}} ^{{k}} \:{f}^{\left({k}\right)} \left(\mathrm{0}\right){sin}\left(\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} {C}_{\mathrm{2}{n}} ^{{k}} \:{f}^{\left({k}\right)} \left(\mathrm{0}\right){sin}\left({n}\pi−\frac{\pi}{\mathrm{2}}\right)\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:{f}^{\left({k}\right)} \left(\mathrm{0}\right) \\ $$$${for}\:{exemple}\:\:{n}=\mathrm{2}\:\Rightarrow{f}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} {C}_{\mathrm{4}} ^{{k}} \:{f}^{\left({k}\right)} \left(\mathrm{0}\right) \\ $$$$={C}_{\mathrm{4}} ^{\mathrm{0}} {f}\left(\mathrm{0}\right)+{C}_{\mathrm{4}} ^{\mathrm{1}} {f}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right)\:+{C}_{\mathrm{4}} ^{\mathrm{2}} {f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)+{C}_{\mathrm{4}} ^{\mathrm{3}} {f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=…\:{and}\:{we}\:{can} \\ $$$${write}\:\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\left(\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:{f}^{\left({k}\right)} \left(\mathrm{0}\right)\right){x}^{\mathrm{2}{n}} \\ $$$$\left.{b}\right)\:{g}\left({x}\right)={e}^{{cos}^{\mathrm{2}} {x}\:} \:\Rightarrow{g}\left({x}\right)\:={e}^{\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \\ $$$$=\sqrt{{e}}×\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{x}\right)} \:\:{and}\:{we}\:{aplly}\:\:{Q}_{{n}} \mathrm{1}…. \\ $$
Commented by abdomathmax last updated on 17/May/20
if you have another way post it...
$${if}\:{you}\:{have}\:{another}\:{way}\:{post}\:{it}… \\ $$
Answered by niroj last updated on 17/May/20
(a) e^(cos x) let, f(x)= e^(cos x) , f(0)=e f_1 (x)=− e^(cos x) .sin x , f_1 (0)=0 f_2 (x)= −[ −e^(cosx) .sin^2 x+ e^(cos x) .cosx)= e^(cos x) sin^2 x−e^(cos x) .cos x f_2 (0)=−e f_3 (x)= −e^(cos x) .sin^3 x+e^(cos x) sin2x f_3 (0)=0 f_4 (x) = e^(cos x) sin^4 x−e^(cos x) .3sin^2 x.cos x−e^(cos x) .sinx.sin2x +2e^(cosx) .cos2x f_4 (0)=2e maclaurin′s series of expansion. f(x)= f(0)+(x/(1!))f_1 (0)+(x^2 /(2!))f_2 (0)+(x^3 /(3!))f_3 (0)+(x^4 /(4!))f_4 (0)+...=. e^(cos x) = e+ x.0+ (x^2 /(2!))(−e)+(x^3 /(3!)).(0)+(x^4 /(4!))(2e)+.... e^(cos x) = e− (1/2)x^2 e+ (2/(4.3.2.1))x^4 e+.... e^(cos x) = e −(1/2)x^2 e + (1/(12))x^4 e+....
$$\:\:\left(\mathrm{a}\right)\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:\:\mathrm{let},\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} ,\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{e} \\ $$$$\:\:\:\:\mathrm{f}_{\mathrm{1}} \left(\mathrm{x}\right)=−\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{sin}\:\mathrm{x}\:,\:\:\:\:\mathrm{f}_{\mathrm{1}} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\:\mathrm{f}_{\mathrm{2}} \left(\mathrm{x}\right)=\:−\left[\:−\mathrm{e}^{\mathrm{cosx}} .\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{cosx}\right)=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\mathrm{f}_{\mathrm{2}} \left(\mathrm{0}\right)=−\mathrm{e} \\ $$$$\:\:\:\mathrm{f}_{\mathrm{3}} \left(\mathrm{x}\right)=\:−\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{sin}^{\mathrm{3}} \:\mathrm{x}+\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \mathrm{sin2x} \\ $$$$\:\:\mathrm{f}_{\mathrm{3}} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\mathrm{f}_{\mathrm{4}} \left(\mathrm{x}\right)\:=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \mathrm{sin}^{\mathrm{4}} \mathrm{x}−\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{3sin}^{\mathrm{2}} \mathrm{x}.\mathrm{cos}\:\mathrm{x}−\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} .\mathrm{sinx}.\mathrm{sin2x}\:+\mathrm{2e}^{\mathrm{cosx}} .\mathrm{cos2x} \\ $$$$\:\:\mathrm{f}_{\mathrm{4}} \left(\mathrm{0}\right)=\mathrm{2e} \\ $$$$\:\mathrm{maclaurin}'\mathrm{s}\:\mathrm{series}\:\mathrm{of}\:\mathrm{expansion}. \\ $$$$\:\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{f}\left(\mathrm{0}\right)+\frac{\mathrm{x}}{\mathrm{1}!}\mathrm{f}_{\mathrm{1}} \left(\mathrm{0}\right)+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\mathrm{f}_{\mathrm{2}} \left(\mathrm{0}\right)+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\mathrm{f}_{\mathrm{3}} \left(\mathrm{0}\right)+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\mathrm{f}_{\mathrm{4}} \left(\mathrm{0}\right)+…=. \\ $$$$\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} =\:\mathrm{e}+\:\mathrm{x}.\mathrm{0}+\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\left(−\mathrm{e}\right)+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}.\left(\mathrm{0}\right)+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\left(\mathrm{2e}\right)+…. \\ $$$$\:\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} =\:\mathrm{e}−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{e}+\:\frac{\mathrm{2}}{\mathrm{4}.\mathrm{3}.\mathrm{2}.\mathrm{1}}\mathrm{x}^{\mathrm{4}} \mathrm{e}+…. \\ $$$$\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \:=\:\mathrm{e}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{e}\:+\:\frac{\mathrm{1}}{\mathrm{12}}\mathrm{x}^{\mathrm{4}} \mathrm{e}+…. \\ $$
Commented by mathmax by abdo last updated on 17/May/20
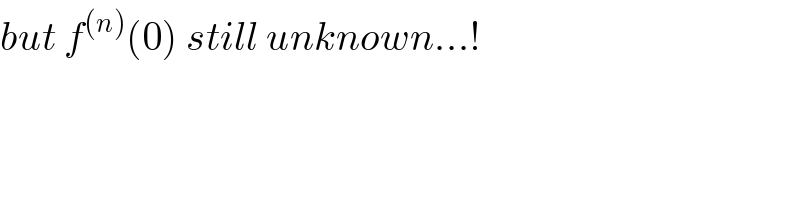
but f^((n)) (0) still unknown...!
$${but}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:{still}\:{unknown}…! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *