Question Number 94212 by abony1303 last updated on 17/May/20
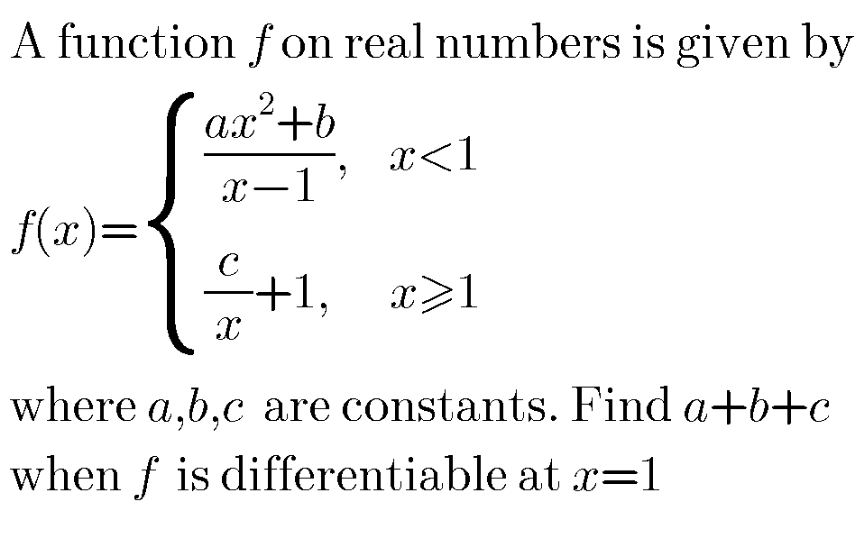
Answered by john santu last updated on 17/May/20
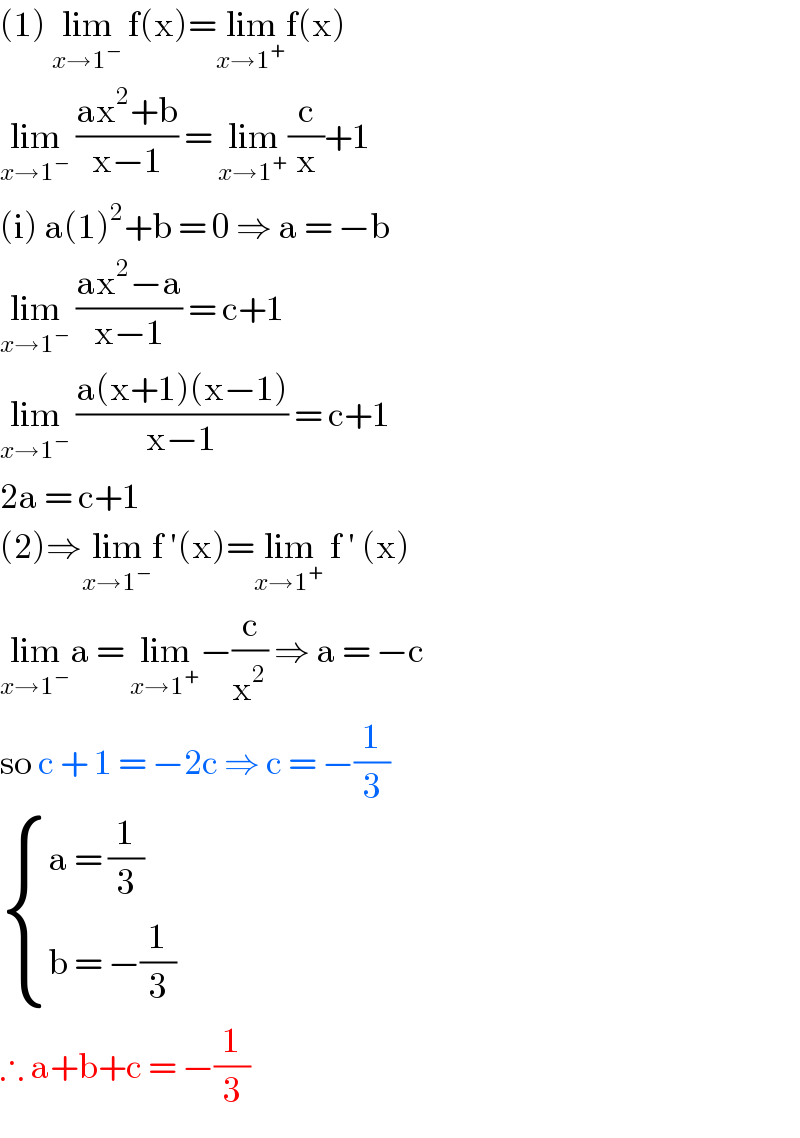
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)=\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}f}\left(\mathrm{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{b}}{\mathrm{x}−\mathrm{1}}\:=\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{\mathrm{c}}{\mathrm{x}}+\mathrm{1} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{a}\left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{b}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{a}\:=\:−\mathrm{b}\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{ax}^{\mathrm{2}} −\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:=\:\mathrm{c}+\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{a}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{x}−\mathrm{1}}\:=\:\mathrm{c}+\mathrm{1} \\ $$$$\mathrm{2a}\:=\:\mathrm{c}+\mathrm{1}\: \\ $$$$\left(\mathrm{2}\right)\Rightarrow\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}f}\:'\left(\mathrm{x}\right)=\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\mathrm{f}\:'\:\left(\mathrm{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}a}\:=\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}−\frac{\mathrm{c}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{a}\:=\:−\mathrm{c}\: \\ $$$$\mathrm{so}\:\mathrm{c}\:+\:\mathrm{1}\:=\:−\mathrm{2c}\:\Rightarrow\:\mathrm{c}\:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\begin{cases}{\mathrm{a}\:=\:\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{b}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}}\end{cases} \\ $$$$\therefore\:\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
