Menu Close

Question-94319

Tinku Tara 0 Comments
Pin




Question Number 94319 by Mozay1 last updated on 18/May/20
Commented by john santu last updated on 18/May/20
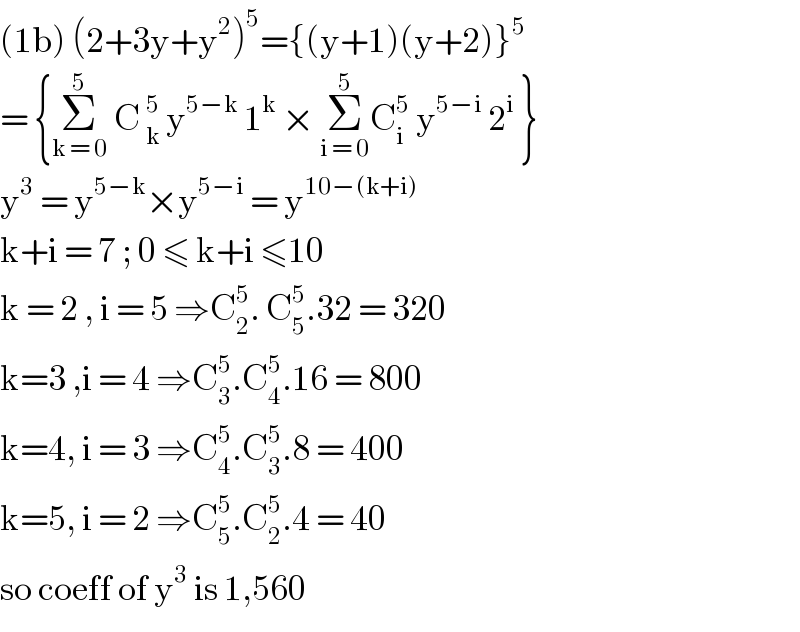
(1b) (2+3y+y^2 )^5 ={(y+1)(y+2)}^5 = {Σ_(k = 0) ^5 C _k^5 y^(5−k) 1^k × Σ_(i = 0) ^5 C_i ^5 y^(5−i) 2^i } y^3 = y^(5−k) ×y^(5−i) = y^(10−(k+i)) k+i = 7 ; 0 ≤ k+i ≤10 k = 2 , i = 5 ⇒C_2 ^5 . C_5 ^5 .32 = 320 k=3 ,i = 4 ⇒C_3 ^5 .C_4 ^5 .16 = 800 k=4, i = 3 ⇒C_4 ^5 .C_3 ^5 .8 = 400 k=5, i = 2 ⇒C_5 ^5 .C_2 ^5 .4 = 40 so coeff of y^3 is 1,560
$$\left(\mathrm{1b}\right)\:\left(\mathrm{2}+\mathrm{3y}+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{5}} =\left\{\left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{y}+\mathrm{2}\right)\right\}^{\mathrm{5}} \\ $$$$=\:\left\{\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\:\mathrm{C}\:_{\mathrm{k}} ^{\mathrm{5}} \:\mathrm{y}^{\mathrm{5}−\mathrm{k}} \:\mathrm{1}^{\mathrm{k}} \:×\:\underset{\mathrm{i}\:=\:\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\mathrm{C}_{\mathrm{i}} ^{\mathrm{5}} \:\mathrm{y}^{\mathrm{5}−\mathrm{i}} \:\mathrm{2}^{\mathrm{i}} \:\right\} \\ $$$$\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{y}^{\mathrm{5}−\mathrm{k}} ×\mathrm{y}^{\mathrm{5}−\mathrm{i}} \:=\:\mathrm{y}^{\mathrm{10}−\left(\mathrm{k}+\mathrm{i}\right)} \\ $$$$\mathrm{k}+\mathrm{i}\:=\:\mathrm{7}\:;\:\mathrm{0}\:\leqslant\:\mathrm{k}+\mathrm{i}\:\leqslant\mathrm{10} \\ $$$$\mathrm{k}\:=\:\mathrm{2}\:,\:\mathrm{i}\:=\:\mathrm{5}\:\Rightarrow\mathrm{C}_{\mathrm{2}} ^{\mathrm{5}} .\:\mathrm{C}_{\mathrm{5}} ^{\mathrm{5}} .\mathrm{32}\:=\:\mathrm{320}\:\: \\ $$$$\mathrm{k}=\mathrm{3}\:,\mathrm{i}\:=\:\mathrm{4}\:\Rightarrow\mathrm{C}_{\mathrm{3}} ^{\mathrm{5}} .\mathrm{C}_{\mathrm{4}} ^{\mathrm{5}} .\mathrm{16}\:=\:\mathrm{800} \\ $$$$\mathrm{k}=\mathrm{4},\:\mathrm{i}\:=\:\mathrm{3}\:\Rightarrow\mathrm{C}_{\mathrm{4}} ^{\mathrm{5}} .\mathrm{C}_{\mathrm{3}} ^{\mathrm{5}} .\mathrm{8}\:=\:\mathrm{400} \\ $$$$\mathrm{k}=\mathrm{5},\:\mathrm{i}\:=\:\mathrm{2}\:\Rightarrow\mathrm{C}_{\mathrm{5}} ^{\mathrm{5}} .\mathrm{C}_{\mathrm{2}} ^{\mathrm{5}} .\mathrm{4}\:=\:\mathrm{40}\: \\ $$$$\mathrm{so}\:\mathrm{coeff}\:\mathrm{of}\:\mathrm{y}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{1},\mathrm{560}\: \\ $$
Commented by mathmax by abdo last updated on 18/May/20
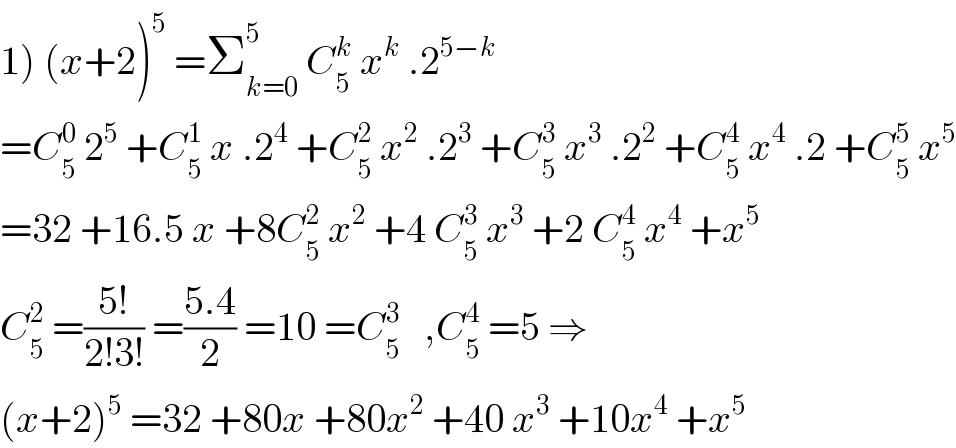
1) (x+2)^5 =Σ_(k=0) ^5 C_5 ^k x^k .2^(5−k) =C_5 ^0 2^5 +C_5 ^1 x .2^4 +C_5 ^2 x^2 .2^3 +C_5 ^3 x^3 .2^2 +C_5 ^4 x^4 .2 +C_5 ^5 x^5 =32 +16.5 x +8C_5 ^2 x^2 +4 C_5 ^3 x^3 +2 C_5 ^4 x^4 +x^5 C_5 ^2 =((5!)/(2!3!)) =((5.4)/2) =10 =C_5 ^3 ,C_5 ^4 =5 ⇒ (x+2)^5 =32 +80x +80x^2 +40 x^3 +10x^4 +x^5
$$\left.\mathrm{1}\right)\:\left({x}+\mathrm{2}\right)^{\mathrm{5}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \:{x}^{{k}} \:.\mathrm{2}^{\mathrm{5}−{k}} \\ $$$$={C}_{\mathrm{5}} ^{\mathrm{0}} \:\mathrm{2}^{\mathrm{5}} \:+{C}_{\mathrm{5}} ^{\mathrm{1}} \:{x}\:.\mathrm{2}^{\mathrm{4}} \:+{C}_{\mathrm{5}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \:.\mathrm{2}^{\mathrm{3}} \:+{C}_{\mathrm{5}} ^{\mathrm{3}} \:{x}^{\mathrm{3}} \:.\mathrm{2}^{\mathrm{2}} \:+{C}_{\mathrm{5}} ^{\mathrm{4}} \:{x}^{\mathrm{4}} \:.\mathrm{2}\:+{C}_{\mathrm{5}} ^{\mathrm{5}} \:{x}^{\mathrm{5}} \\ $$$$=\mathrm{32}\:+\mathrm{16}.\mathrm{5}\:{x}\:+\mathrm{8}{C}_{\mathrm{5}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \:+\mathrm{4}\:{C}_{\mathrm{5}} ^{\mathrm{3}} \:{x}^{\mathrm{3}} \:+\mathrm{2}\:{C}_{\mathrm{5}} ^{\mathrm{4}} \:{x}^{\mathrm{4}} \:+{x}^{\mathrm{5}} \\ $$$${C}_{\mathrm{5}} ^{\mathrm{2}} \:=\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{3}!}\:=\frac{\mathrm{5}.\mathrm{4}}{\mathrm{2}}\:=\mathrm{10}\:={C}_{\mathrm{5}} ^{\mathrm{3}} \:\:\:,{C}_{\mathrm{5}} ^{\mathrm{4}} \:=\mathrm{5}\:\Rightarrow \\ $$$$\left({x}+\mathrm{2}\right)^{\mathrm{5}} \:=\mathrm{32}\:+\mathrm{80}{x}\:+\mathrm{80}{x}^{\mathrm{2}} \:+\mathrm{40}\:{x}^{\mathrm{3}} \:+\mathrm{10}{x}^{\mathrm{4}} \:+{x}^{\mathrm{5}} \\ $$
Commented by mathmax by abdo last updated on 18/May/20
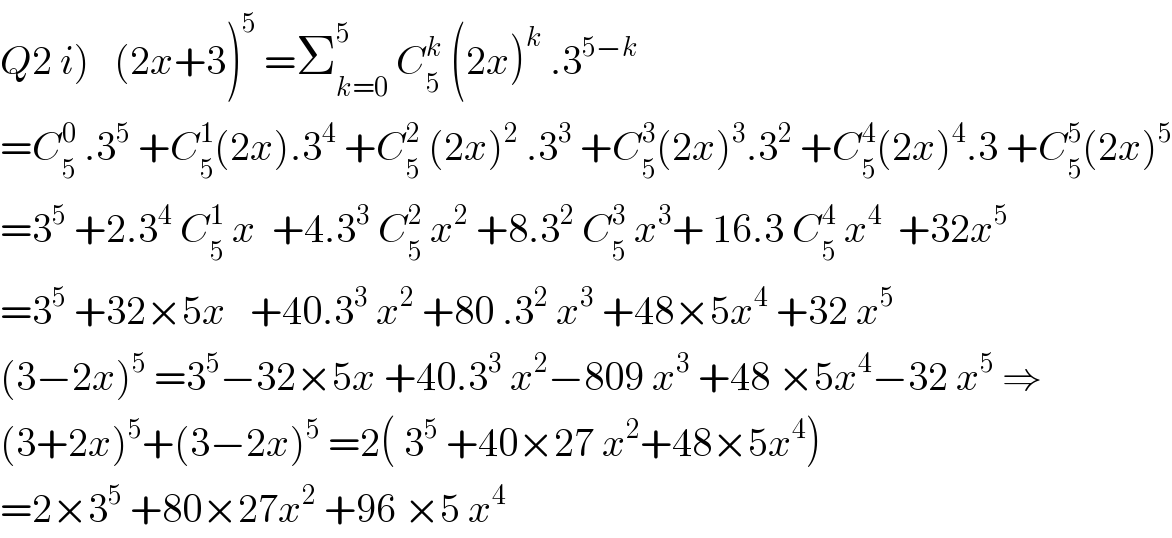
Q2 i) (2x+3)^5 =Σ_(k=0) ^5 C_5 ^k (2x)^k .3^(5−k) =C_5 ^0 .3^5 +C_5 ^1 (2x).3^4 +C_5 ^2 (2x)^2 .3^3 +C_5 ^3 (2x)^3 .3^2 +C_5 ^4 (2x)^4 .3 +C_5 ^5 (2x)^5 =3^5 +2.3^4 C_5 ^1 x +4.3^3 C_5 ^2 x^2 +8.3^2 C_5 ^3 x^3 + 16.3 C_5 ^4 x^4 +32x^5 =3^5 +32×5x +40.3^3 x^2 +80 .3^2 x^3 +48×5x^4 +32 x^5 (3−2x)^5 =3^5 −32×5x +40.3^3 x^2 −809 x^3 +48 ×5x^4 −32 x^5 ⇒ (3+2x)^5 +(3−2x)^5 =2( 3^5 +40×27 x^2 +48×5x^4 ) =2×3^5 +80×27x^2 +96 ×5 x^4
$$\left.{Q}\mathrm{2}\:{i}\right)\:\:\:\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{5}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \:\left(\mathrm{2}{x}\right)^{{k}} \:.\mathrm{3}^{\mathrm{5}−{k}} \\ $$$$={C}_{\mathrm{5}} ^{\mathrm{0}} \:.\mathrm{3}^{\mathrm{5}} \:+{C}_{\mathrm{5}} ^{\mathrm{1}} \left(\mathrm{2}{x}\right).\mathrm{3}^{\mathrm{4}} \:+{C}_{\mathrm{5}} ^{\mathrm{2}} \:\left(\mathrm{2}{x}\right)^{\mathrm{2}} \:.\mathrm{3}^{\mathrm{3}} \:+{C}_{\mathrm{5}} ^{\mathrm{3}} \left(\mathrm{2}{x}\right)^{\mathrm{3}} .\mathrm{3}^{\mathrm{2}} \:+{C}_{\mathrm{5}} ^{\mathrm{4}} \left(\mathrm{2}{x}\right)^{\mathrm{4}} .\mathrm{3}\:+{C}_{\mathrm{5}} ^{\mathrm{5}} \left(\mathrm{2}{x}\right)^{\mathrm{5}} \\ $$$$=\mathrm{3}^{\mathrm{5}} \:+\mathrm{2}.\mathrm{3}^{\mathrm{4}} \:{C}_{\mathrm{5}} ^{\mathrm{1}} \:{x}\:\:+\mathrm{4}.\mathrm{3}^{\mathrm{3}} \:{C}_{\mathrm{5}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \:+\mathrm{8}.\mathrm{3}^{\mathrm{2}} \:{C}_{\mathrm{5}} ^{\mathrm{3}} \:{x}^{\mathrm{3}} +\:\mathrm{16}.\mathrm{3}\:{C}_{\mathrm{5}} ^{\mathrm{4}} \:{x}^{\mathrm{4}} \:\:+\mathrm{32}{x}^{\mathrm{5}} \\ $$$$=\mathrm{3}^{\mathrm{5}} \:+\mathrm{32}×\mathrm{5}{x}\:\:\:+\mathrm{40}.\mathrm{3}^{\mathrm{3}} \:{x}^{\mathrm{2}} \:+\mathrm{80}\:.\mathrm{3}^{\mathrm{2}} \:{x}^{\mathrm{3}} \:+\mathrm{48}×\mathrm{5}{x}^{\mathrm{4}} \:+\mathrm{32}\:{x}^{\mathrm{5}} \: \\ $$$$\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{5}} \:=\mathrm{3}^{\mathrm{5}} −\mathrm{32}×\mathrm{5}{x}\:+\mathrm{40}.\mathrm{3}^{\mathrm{3}} \:{x}^{\mathrm{2}} −\mathrm{809}\:{x}^{\mathrm{3}} \:+\mathrm{48}\:×\mathrm{5}{x}^{\mathrm{4}} −\mathrm{32}\:{x}^{\mathrm{5}} \:\Rightarrow \\ $$$$\left(\mathrm{3}+\mathrm{2}{x}\right)^{\mathrm{5}} +\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{5}} \:=\mathrm{2}\left(\:\mathrm{3}^{\mathrm{5}} \:+\mathrm{40}×\mathrm{27}\:{x}^{\mathrm{2}} +\mathrm{48}×\mathrm{5}{x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{2}×\mathrm{3}^{\mathrm{5}} \:+\mathrm{80}×\mathrm{27}{x}^{\mathrm{2}} \:+\mathrm{96}\:×\mathrm{5}\:{x}^{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 18/May/20
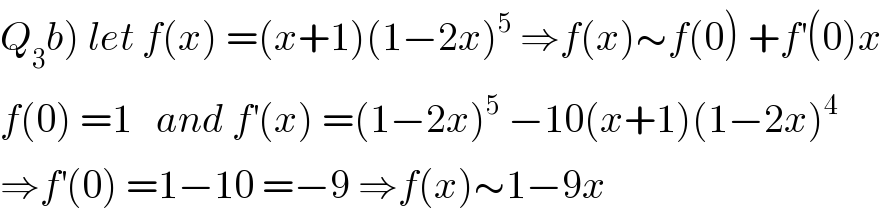
Q_3 b) let f(x) =(x+1)(1−2x)^5 ⇒f(x)∼f(0) +f^′ (0)x f(0) =1 and f^′ (x) =(1−2x)^5 −10(x+1)(1−2x)^4 ⇒f^′ (0) =1−10 =−9 ⇒f(x)∼1−9x
$$\left.{Q}_{\mathrm{3}} {b}\right)\:{let}\:{f}\left({x}\right)\:=\left({x}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{5}} \:\Rightarrow{f}\left({x}\right)\sim{f}\left(\mathrm{0}\right)\:+{f}^{'} \left(\mathrm{0}\right){x} \\ $$$${f}\left(\mathrm{0}\right)\:=\mathrm{1}\:\:\:{and}\:{f}^{'} \left({x}\right)\:=\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{5}} \:−\mathrm{10}\left({x}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{4}} \\ $$$$\Rightarrow{f}^{'} \left(\mathrm{0}\right)\:=\mathrm{1}−\mathrm{10}\:=−\mathrm{9}\:\Rightarrow{f}\left({x}\right)\sim\mathrm{1}−\mathrm{9}{x}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *