Question Number 94397 by peter frank last updated on 18/May/20
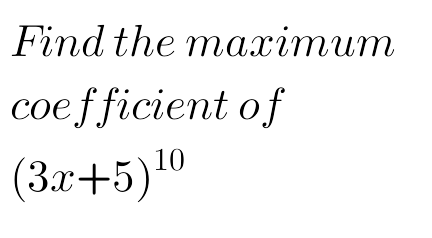
Answered by mr W last updated on 18/May/20
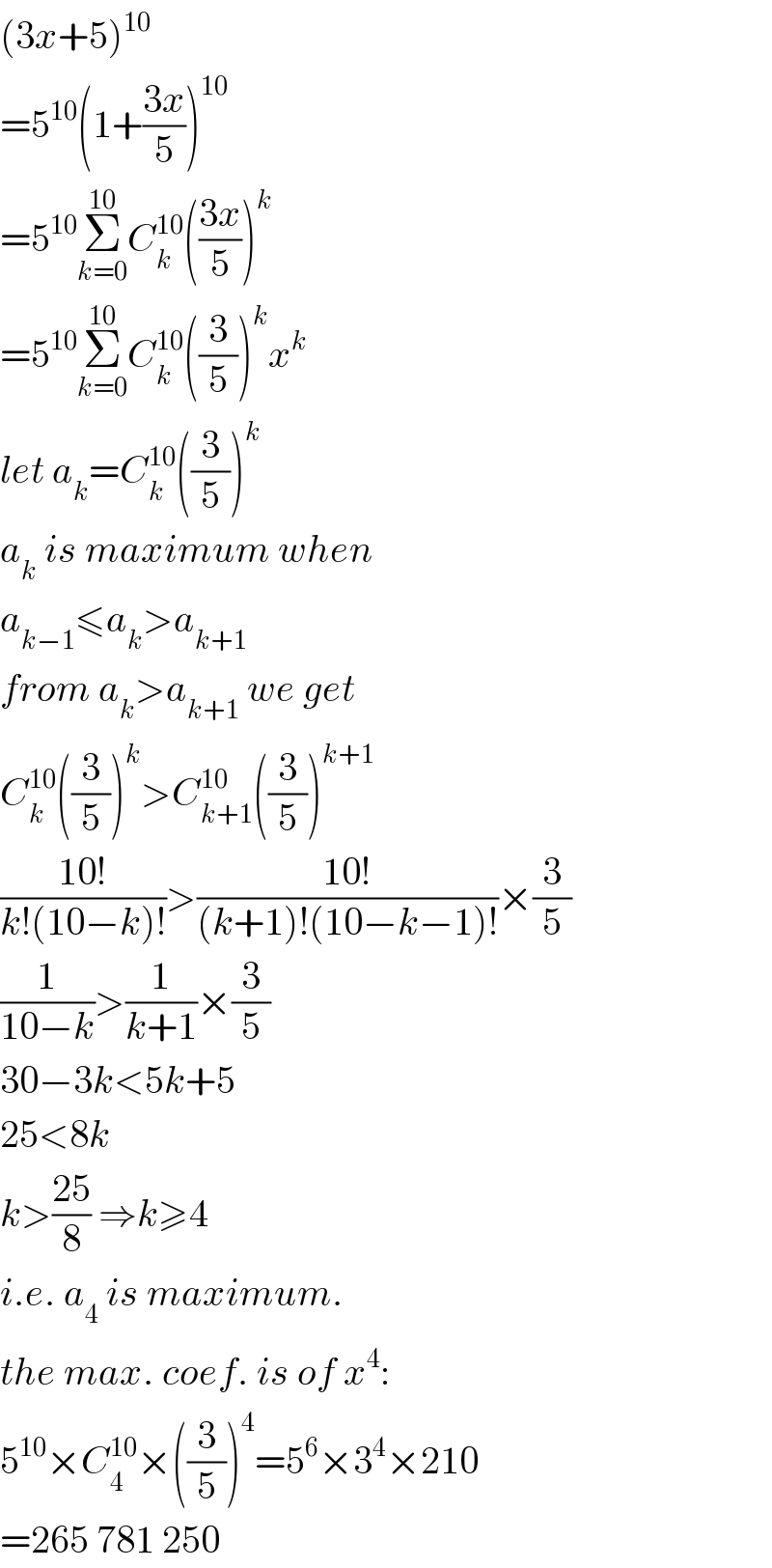
$$\left(\mathrm{3}{x}+\mathrm{5}\right)^{\mathrm{10}} \\ $$$$=\mathrm{5}^{\mathrm{10}} \left(\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{5}}\right)^{\mathrm{10}} \\ $$$$=\mathrm{5}^{\mathrm{10}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}{C}_{{k}} ^{\mathrm{10}} \left(\frac{\mathrm{3}{x}}{\mathrm{5}}\right)^{{k}} \\ $$$$=\mathrm{5}^{\mathrm{10}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}{C}_{{k}} ^{\mathrm{10}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{k}} {x}^{{k}} \\ $$$${let}\:{a}_{{k}} ={C}_{{k}} ^{\mathrm{10}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{k}} \\ $$$${a}_{{k}} \:{is}\:{maximum}\:{when} \\ $$$${a}_{{k}−\mathrm{1}} \leqslant{a}_{{k}} >{a}_{{k}+\mathrm{1}} \\ $$$${from}\:{a}_{{k}} >{a}_{{k}+\mathrm{1}} \:{we}\:{get} \\ $$$${C}_{{k}} ^{\mathrm{10}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{k}} >{C}_{{k}+\mathrm{1}} ^{\mathrm{10}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{k}+\mathrm{1}} \\ $$$$\frac{\mathrm{10}!}{{k}!\left(\mathrm{10}−{k}\right)!}>\frac{\mathrm{10}!}{\left({k}+\mathrm{1}\right)!\left(\mathrm{10}−{k}−\mathrm{1}\right)!}×\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\mathrm{1}}{\mathrm{10}−{k}}>\frac{\mathrm{1}}{{k}+\mathrm{1}}×\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{30}−\mathrm{3}{k}<\mathrm{5}{k}+\mathrm{5} \\ $$$$\mathrm{25}<\mathrm{8}{k} \\ $$$${k}>\frac{\mathrm{25}}{\mathrm{8}}\:\Rightarrow{k}\geqslant\mathrm{4} \\ $$$${i}.{e}.\:{a}_{\mathrm{4}} \:{is}\:{maximum}. \\ $$$${the}\:{max}.\:{coef}.\:{is}\:{of}\:{x}^{\mathrm{4}} : \\ $$$$\mathrm{5}^{\mathrm{10}} ×{C}_{\mathrm{4}} ^{\mathrm{10}} ×\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{4}} =\mathrm{5}^{\mathrm{6}} ×\mathrm{3}^{\mathrm{4}} ×\mathrm{210} \\ $$$$=\mathrm{265}\:\mathrm{781}\:\mathrm{250} \\ $$
Commented by peter frank last updated on 19/May/20
$${thank}\:{you}\:{sir} \\ $$
