Question-94448

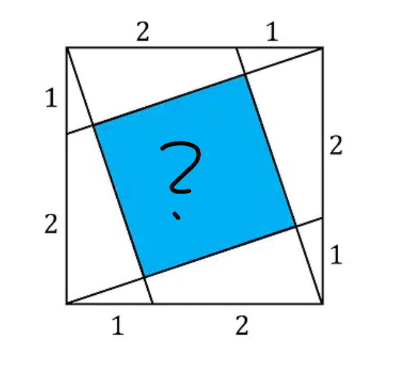
Question Number 94448 by mr W last updated on 18/May/20

Commented by behi83417@gmail.com last updated on 18/May/20

Commented by behi83417@gmail.com last updated on 19/May/20

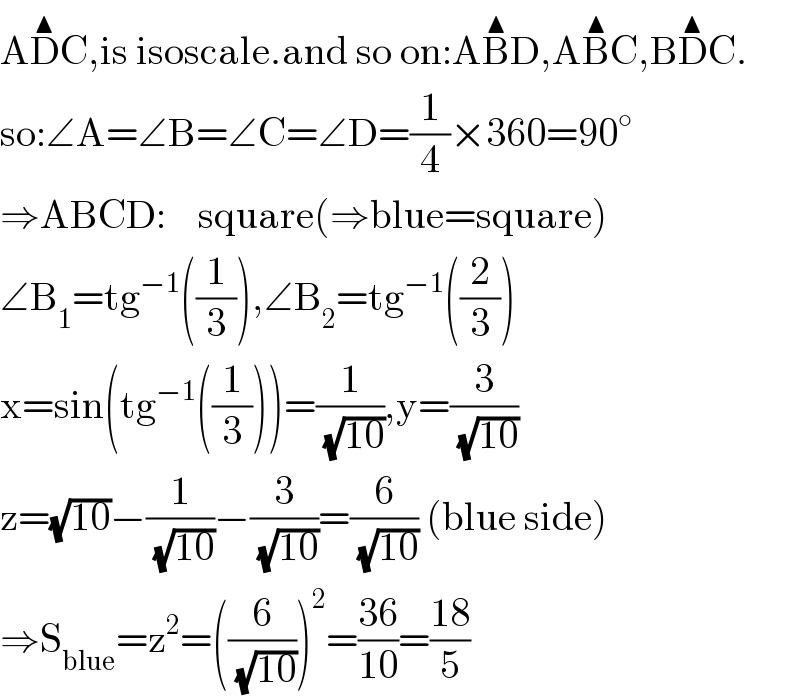
AD^▲ C,is isoscale.and so on:AB^▲ D,AB^▲ C,BD^▲ C. so:∠A=∠B=∠C=∠D=(1/4)×360=90^○ ⇒ABCD: square(⇒blue=square) ∠B_1 =tg^(−1) ((1/3)),∠B_2 =tg^(−1) ((2/3)) x=sin(tg^(−1) ((1/3)))=(1/( (√(10)))),y=(3/( (√(10)))) z=(√(10))−(1/( (√(10))))−(3/( (√(10))))=(6/( (√(10)))) (blue side) ⇒S_(blue) =z^2 =((6/( (√(10)))))^2 =((36)/(10))=((18)/5)

$$\mathrm{A}\overset{\blacktriangle} {\mathrm{D}C},\mathrm{is}\:\mathrm{isoscale}.\mathrm{and}\:\mathrm{so}\:\mathrm{on}:\mathrm{A}\overset{\blacktriangle} {\mathrm{B}D},\mathrm{A}\overset{\blacktriangle} {\mathrm{B}C},\mathrm{B}\overset{\blacktriangle} {\mathrm{D}C}. \\ $$$$\mathrm{so}:\angle\mathrm{A}=\angle\mathrm{B}=\angle\mathrm{C}=\angle\mathrm{D}=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{360}=\mathrm{90}^{\circ} \\ $$$$\Rightarrow\mathrm{ABCD}:\:\:\:\:\mathrm{square}\left(\Rightarrow\mathrm{blue}=\mathrm{square}\right) \\ $$$$\angle\mathrm{B}_{\mathrm{1}} =\mathrm{tg}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right),\angle\mathrm{B}_{\mathrm{2}} =\mathrm{tg}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$\mathrm{x}=\mathrm{sin}\left(\mathrm{tg}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}},\mathrm{y}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{z}=\sqrt{\mathrm{10}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{10}}}\:\left(\mathrm{blue}\:\mathrm{side}\right) \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{blue}} =\mathrm{z}^{\mathrm{2}} =\left(\frac{\mathrm{6}}{\:\sqrt{\mathrm{10}}}\right)^{\mathrm{2}} =\frac{\mathrm{36}}{\mathrm{10}}=\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Answered by MJS last updated on 18/May/20

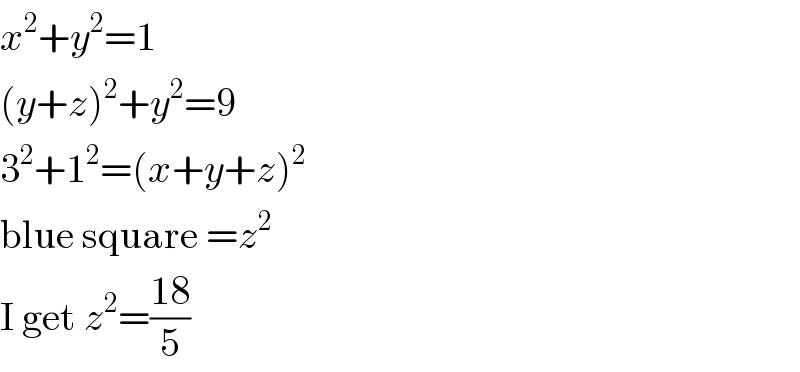
x^2 +y^2 =1 (y+z)^2 +y^2 =9 3^2 +1^2 =(x+y+z)^2 blue square =z^2 I get z^2 =((18)/5)

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({y}+{z}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} =\left({x}+{y}+{z}\right)^{\mathrm{2}} \\ $$$$\mathrm{blue}\:\mathrm{square}\:={z}^{\mathrm{2}} \\ $$$$\mathrm{I}\:\mathrm{get}\:{z}^{\mathrm{2}} =\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Answered by john santu last updated on 19/May/20

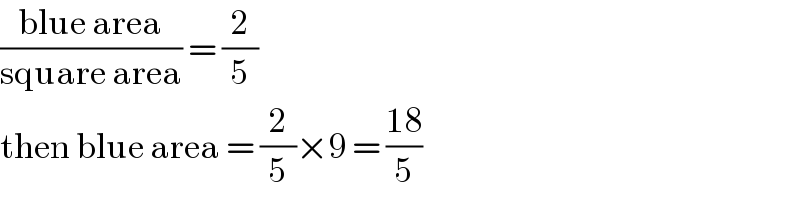
((blue area)/(square area)) = (2/5) then blue area = (2/5)×9 = ((18)/5)

$$\frac{\mathrm{blue}\:\mathrm{area}}{\mathrm{square}\:\mathrm{area}}\:=\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{then}\:\mathrm{blue}\:\mathrm{area}\:=\:\frac{\mathrm{2}}{\mathrm{5}}×\mathrm{9}\:=\:\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 19/May/20

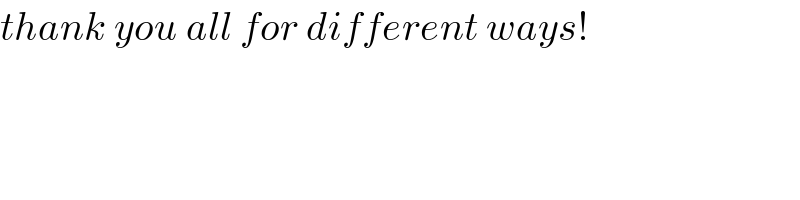
$${thank}\:{you}\:{all}\:{for}\:{different}\:{ways}! \\ $$

Answered by mr W last updated on 19/May/20

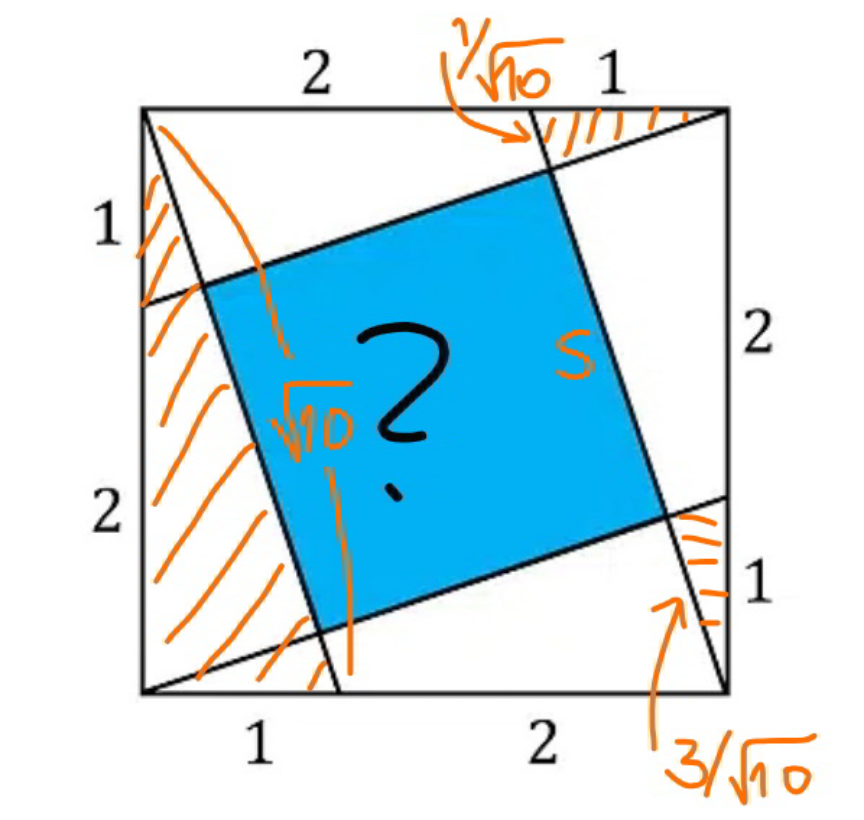
Commented by mr W last updated on 19/May/20

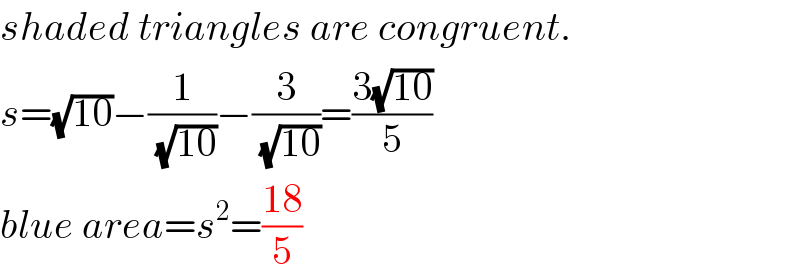
shaded triangles are congruent. s=(√(10))−(1/( (√(10))))−(3/( (√(10))))=((3(√(10)))/5) blue area=s^2 =((18)/5)

$${shaded}\:{triangles}\:{are}\:{congruent}. \\ $$$${s}=\sqrt{\mathrm{10}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{5}} \\ $$$${blue}\:{area}={s}^{\mathrm{2}} =\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 19/May/20

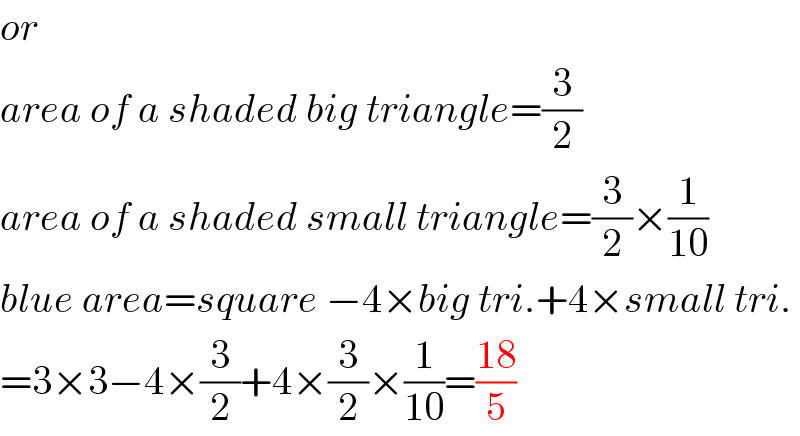
or area of a shaded big triangle=(3/2) area of a shaded small triangle=(3/2)×(1/(10)) blue area=square −4×big tri.+4×small tri. =3×3−4×(3/2)+4×(3/2)×(1/(10))=((18)/5)

$${or} \\ $$$${area}\:{of}\:{a}\:{shaded}\:{big}\:{triangle}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${area}\:{of}\:{a}\:{shaded}\:{small}\:{triangle}=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${blue}\:{area}={square}\:−\mathrm{4}×{big}\:{tri}.+\mathrm{4}×{small}\:{tri}. \\ $$$$=\mathrm{3}×\mathrm{3}−\mathrm{4}×\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{4}×\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{10}}=\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/May/20

Actually I am waiting for something different like this.

$$\mathrm{Actually}\:\mathrm{I}\:\mathrm{am}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{something}\:\mathrm{different} \\ $$$$\mathrm{like}\:\mathrm{this}.\: \\ $$

Commented by mr W last updated on 19/May/20

$${please}\:{show}\:{us}\:{this}\:{something}\:{different} \\ $$$${sir}!\: \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/May/20

tanθ = (1/3) ⇒ cos θ=(3/( (√(10)))) AP=cos θ, AQ=3cos θ ∴ PQ=AQ−AP=2cos θ ∴PQ=(6/( (√(10)))) ∴ Area=((36)/(10)) = ((18)/5) this is my try sir

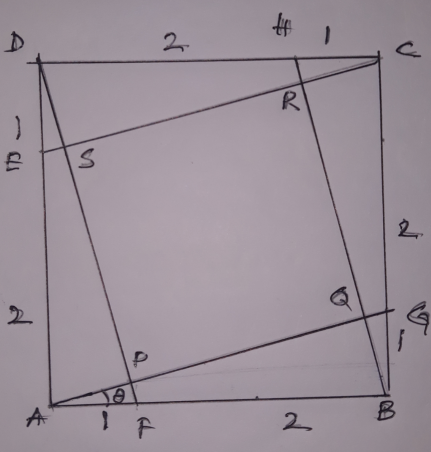
$$\mathrm{tan}\theta\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\Rightarrow\:\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{AP}=\mathrm{cos}\:\theta,\:\mathrm{AQ}=\mathrm{3cos}\:\theta\:\therefore\:\mathrm{PQ}=\mathrm{AQ}−\mathrm{AP}=\mathrm{2cos}\:\theta \\ $$$$\therefore\mathrm{PQ}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{10}}}\:\:\therefore\:\mathrm{Area}=\frac{\mathrm{36}}{\mathrm{10}}\:=\:\frac{\mathrm{18}}{\mathrm{5}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{my}\:\mathrm{try}\:\mathrm{sir} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/May/20

Commented by PRITHWISH SEN 2 last updated on 19/May/20

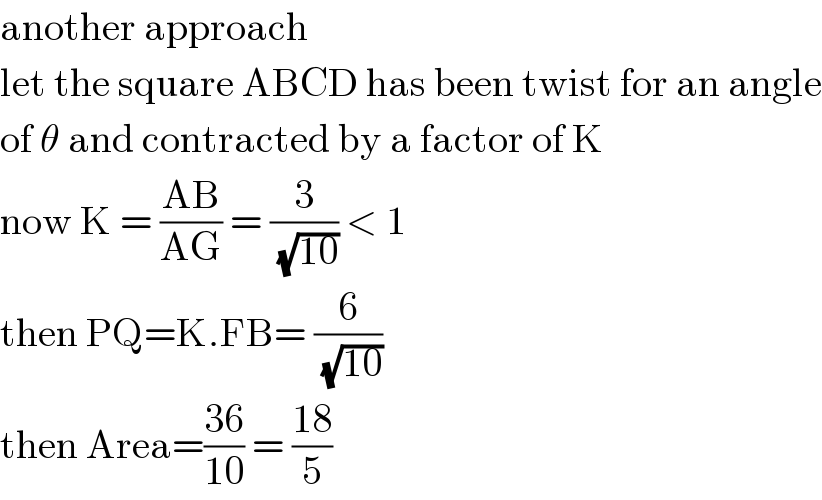
another approach let the square ABCD has been twist for an angle of θ and contracted by a factor of K now K = ((AB)/(AG)) = (3/( (√(10)))) < 1 then PQ=K.FB= (6/( (√(10)))) then Area=((36)/(10)) = ((18)/5)

$$\mathrm{another}\:\mathrm{approach} \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{square}\:\mathrm{ABCD}\:\mathrm{has}\:\mathrm{been}\:\mathrm{twist}\:\mathrm{for}\:\mathrm{an}\:\mathrm{angle} \\ $$$$\mathrm{of}\:\theta\:\mathrm{and}\:\mathrm{contracted}\:\mathrm{by}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{K} \\ $$$$\mathrm{now}\:\mathrm{K}\:=\:\frac{\mathrm{AB}}{\mathrm{AG}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:<\:\mathrm{1}\: \\ $$$$\mathrm{then}\:\mathrm{PQ}=\mathrm{K}.\mathrm{FB}=\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{then}\:\mathrm{Area}=\frac{\mathrm{36}}{\mathrm{10}}\:=\:\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/May/20

Let B be a complex number on the complex plane with AB as a real axis and A as the origin then B = 3e^(i0) now a complex number is multiplied which effect a contraction then let the number be re^(i𝛉) ∴ Q=3re^(i𝛉) ⇒ ∣AQ∣=3r = (9/( (√(10)))) then r=(3/( (√(10)))) now if another complex number 2e^(i0) be multiplied by the same complex number then it turns to = 2re^(i𝛉) now ∣2re^(i𝛉) ∣= ∣PQ∣=(6/( (√(10)))) ∴the Area=(PQ)^2 = ((18)/5)

$$\mathrm{Let}\:\mathrm{B}\:\mathrm{be}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{on}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{plane} \\ $$$$\mathrm{with}\:\mathrm{AB}\:\mathrm{as}\:\mathrm{a}\:\mathrm{real}\:\mathrm{axis}\:\mathrm{and}\:\mathrm{A}\:\mathrm{as}\:\mathrm{the}\:\mathrm{origin} \\ $$$$\mathrm{then}\:\mathrm{B}\:=\:\mathrm{3e}^{\boldsymbol{\mathrm{i}}\mathrm{0}} \\ $$$$\mathrm{now}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{is}\:\mathrm{multiplied}\:\mathrm{which}\:\mathrm{effect} \\ $$$$\mathrm{a}\:\mathrm{contraction}\: \\ $$$$\mathrm{then}\:\mathrm{let}\:\mathrm{the}\:\mathrm{number}\:\mathrm{be}\:\mathrm{re}^{\boldsymbol{\mathrm{i}\theta}} \\ $$$$\therefore\:\mathrm{Q}=\mathrm{3re}^{\boldsymbol{\mathrm{i}\theta}} \:\:\:\:\Rightarrow\:\mid\mathrm{AQ}\mid=\mathrm{3r}\:=\:\frac{\mathrm{9}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{then}\:\mathrm{r}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:\:\mathrm{now}\:\mathrm{if}\:\mathrm{another}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{2e}^{\boldsymbol{\mathrm{i}}\mathrm{0}} \mathrm{be}\:\mathrm{multiplied}\:\mathrm{by}\:\mathrm{the}\:\mathrm{same}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{then}\:\mathrm{it}\:\mathrm{turns}\:\mathrm{to}\:=\:\mathrm{2re}^{\boldsymbol{\mathrm{i}\theta}} \\ $$$$\mathrm{now}\:\mid\mathrm{2re}^{\boldsymbol{\mathrm{i}\theta}} \mid=\:\mid\mathrm{PQ}\mid=\frac{\mathrm{6}}{\:\sqrt{\mathrm{10}}}\: \\ $$$$\therefore\mathrm{the}\:\mathrm{Area}=\left(\mathrm{PQ}\right)^{\mathrm{2}} =\:\frac{\mathrm{18}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 19/May/20

$${great}! \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/May/20

No sir ,yours is beautiful as it is simple. I wish one day I will able to think like you. Thank you sir.

$$\mathrm{No}\:\mathrm{sir}\:,\mathrm{yours}\:\mathrm{is}\:\mathrm{beautiful}\:\mathrm{as}\:\mathrm{it}\:\mathrm{is}\:\mathrm{simple}.\:\mathrm{I}\:\mathrm{wish} \\ $$$$\mathrm{one}\:\mathrm{day}\:\mathrm{I}\:\mathrm{will}\:\:\mathrm{able}\:\mathrm{to}\:\mathrm{think}\:\mathrm{like}\:\mathrm{you}.\:\mathrm{Thank}\:\mathrm{you} \\ $$$$\mathrm{sir}. \\ $$

Commented by mr W last updated on 19/May/20

$${sometimes}\:{it}'{s}\:{a}\:{nice}\:{feeling}\:{to} \\ $$$${search}\:{for}\:{or}\:{even}\:{to}\:{find}\:{that} \\ $$$${something}\:{different}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply