Question-94528

Question Number 94528 by i jagooll last updated on 19/May/20

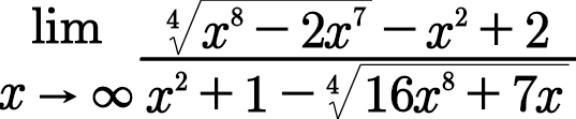
Commented by i jagooll last updated on 19/May/20

lim_(x→∞) ((x^2 {((1−(2/x)))^(1/(4 )) −1+(2/x^2 )})/(x^2 {1+(1/x^2 )−((16+(7/x^7 )))^(1/(4 )) })) = 0

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \:\left\{\sqrt[{\mathrm{4}\:\:}]{\mathrm{1}−\frac{\mathrm{2}}{{x}}}−\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right\}}{{x}^{\mathrm{2}} \left\{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\sqrt[{\mathrm{4}\:\:}]{\mathrm{16}+\frac{\mathrm{7}}{{x}^{\mathrm{7}} }}\right\}}\:=\:\mathrm{0} \\ $$$$ \\ $$

Answered by abdomathmax last updated on 20/May/20

let f(x)=(((x^8 −2x^7 )^(1/4) +2−x^2 )/(x^2 +1−(16x^8 +7x)^(1/4) )) lim_∞ f(x)? f(x) =((x^2 (1−(2/x))^(1/4) +2−x^2 )/(x^2 +1−2x^2 (1+(7/(16x)))^(1/4) )) ⇒ f(x)∼((x^2 (1−(1/(2x)))+2−x^2 )/(x^2 +1−2x^2 (1+(7/(64x))))) =((x^2 −(x/2)+2−x^2 )/(x^2 +1−2x^2 −((7x)/(32)))) =((−(x/2)+2)/(−x^2 −((7x)/(32))+1)) ⇒lim_(x→∞) f(x) =lim_(x→∞) ((−x)/(−2x^2 )) =lim_(x→∞) (1/(2x)) =0

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{x}^{\mathrm{8}} −\mathrm{2x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{2}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\left(\mathrm{16x}^{\mathrm{8}} \:+\mathrm{7x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\:\mathrm{lim}_{\infty} \mathrm{f}\left(\mathrm{x}\right)? \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:+\mathrm{2}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{7}}{\mathrm{16x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2x}}\right)+\mathrm{2}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{7}}{\mathrm{64x}}\right)}\:=\frac{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{2}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} −\frac{\mathrm{7x}}{\mathrm{32}}} \\ $$$$=\frac{−\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{2}}{−\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{7x}}{\mathrm{32}}+\mathrm{1}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{−\mathrm{x}}{−\mathrm{2x}^{\mathrm{2}} } \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \:\frac{\mathrm{1}}{\mathrm{2x}}\:=\mathrm{0} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply