Question Number 94679 by i jagooll last updated on 20/May/20
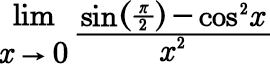
Commented by i jagooll last updated on 20/May/20
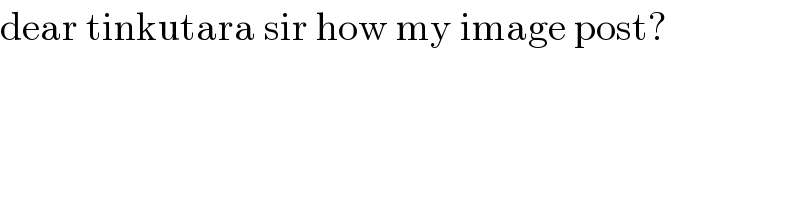
$$\mathrm{dear}\:\mathrm{tinkutara}\:\mathrm{sir}\:\mathrm{how}\:\mathrm{my}\:\mathrm{image}\:\mathrm{post}? \\ $$
Commented by i jagooll last updated on 20/May/20

$$\mathrm{thank}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 20/May/20
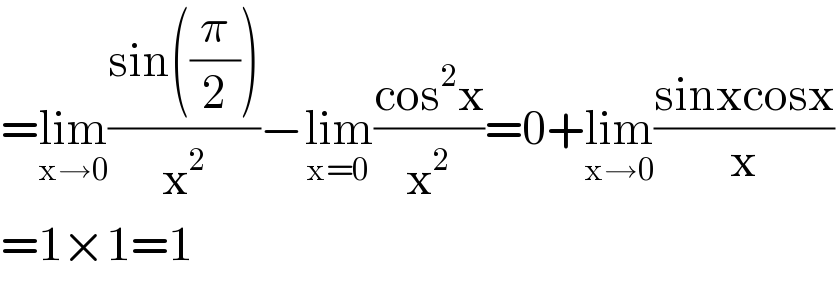
$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right)}{\mathrm{x}^{\mathrm{2}} }−\underset{\mathrm{x}=\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{0}+\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sinxcosx}}{\mathrm{x}} \\ $$$$=\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$
Commented by i jagooll last updated on 20/May/20
cool man ����
Answered by mathmax by abdo last updated on 20/May/20
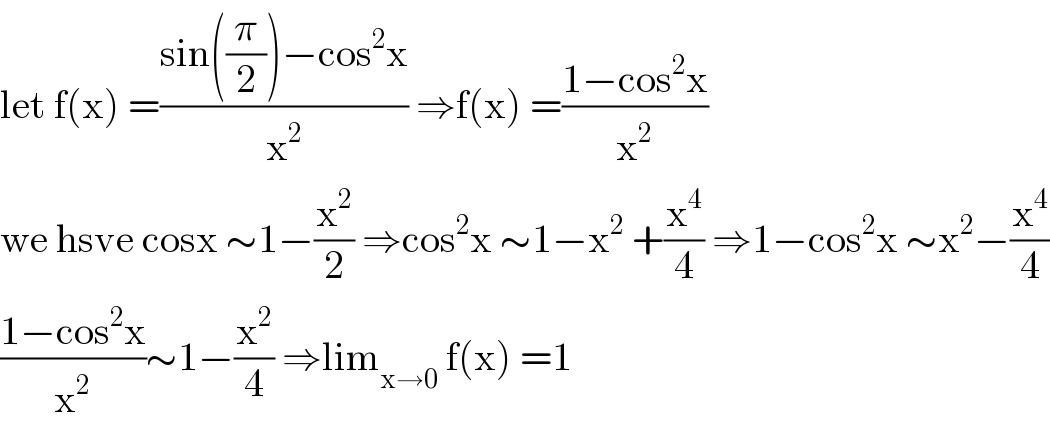
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{hsve}\:\mathrm{cosx}\:\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\sim\mathrm{1}−\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}}\:\Rightarrow\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\sim\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$
