Question-94730

Question Number 94730 by i jagooll last updated on 20/May/20

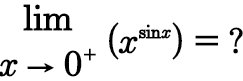
Answered by john santu last updated on 20/May/20

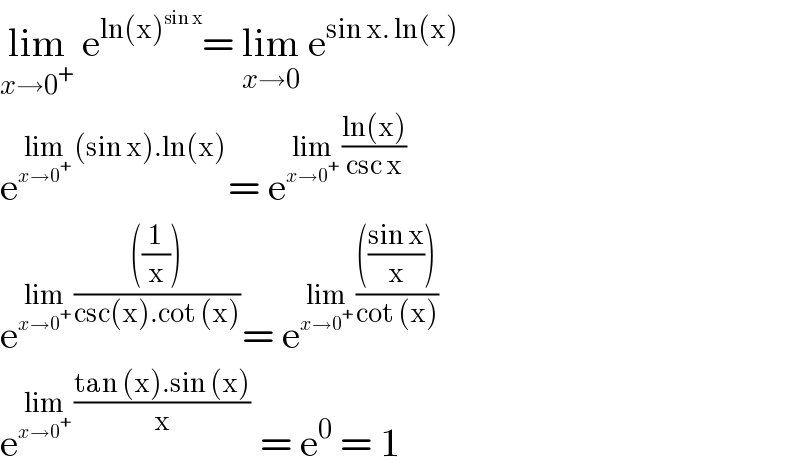
lim_(x→0^+ ) e^(ln(x)^(sin x) ) = lim_(x→0) e^(sin x. ln(x)) e^(lim_(x→0^+ ) (sin x).ln(x)) = e^(lim_(x→0^+ ) ((ln(x))/(csc x))) e^(lim_(x→0^+ ) ((((1/x)))/(csc(x).cot (x)))) = e^(lim_(x→0^+ ) (((((sin x)/x)))/(cot (x)))) e^(lim_(x→0^+ ) ((tan (x).sin (x))/x)) = e^0 = 1

$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\mathrm{e}^{\mathrm{ln}\left(\mathrm{x}\right)^{\mathrm{sin}\:\mathrm{x}} } =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{e}^{\mathrm{sin}\:\mathrm{x}.\:\mathrm{ln}\left(\mathrm{x}\right)} \\ $$$$\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\mathrm{sin}\:\mathrm{x}\right).\mathrm{ln}\left(\mathrm{x}\right)} =\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{csc}\:\mathrm{x}}} \\ $$$$\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{csc}\left(\mathrm{x}\right).\mathrm{cot}\:\left(\mathrm{x}\right)}} =\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)}{\mathrm{cot}\:\left(\mathrm{x}\right)}} \\ $$$$\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{x}\right).\mathrm{sin}\:\left(\mathrm{x}\right)}{\mathrm{x}}} \:=\:\mathrm{e}^{\mathrm{0}} \:=\:\mathrm{1}\: \\ $$

Commented by john santu last updated on 20/May/20

$$\mathrm{correct}? \\ $$

Commented by i jagooll last updated on 21/May/20

$$\mathrm{yes}..\mathrm{correct} \\ $$

Answered by mathmax by abdo last updated on 21/May/20

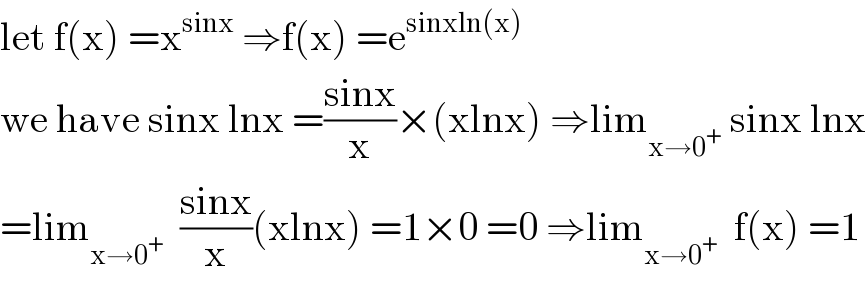
let f(x) =x^(sinx) ⇒f(x) =e^(sinxln(x)) we have sinx lnx =((sinx)/x)×(xlnx) ⇒lim_(x→0^+ ) sinx lnx =lim_(x→0^+ ) ((sinx)/x)(xlnx) =1×0 =0 ⇒lim_(x→0^+ ) f(x) =1

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{sinx}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{sinxln}\left(\mathrm{x}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{sinx}\:\mathrm{lnx}\:=\frac{\mathrm{sinx}}{\mathrm{x}}×\left(\mathrm{xlnx}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\mathrm{sinx}\:\mathrm{lnx} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\mathrm{sinx}}{\mathrm{x}}\left(\mathrm{xlnx}\right)\:=\mathrm{1}×\mathrm{0}\:=\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply