Question-94739

Question Number 94739 by 174 last updated on 20/May/20

Commented by i jagooll last updated on 20/May/20

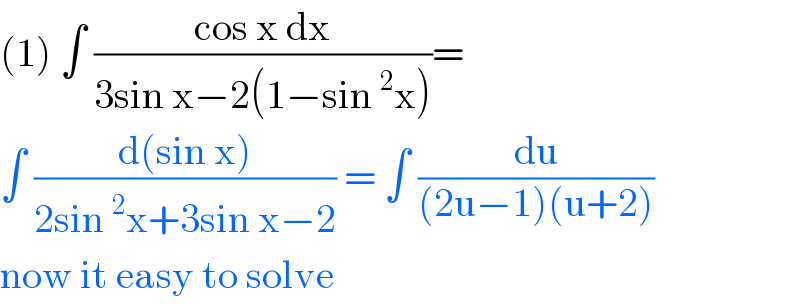
(1) ∫ ((cos x dx)/(3sin x−2(1−sin^2 x)))= ∫ ((d(sin x))/(2sin^2 x+3sin x−2)) = ∫ (du/((2u−1)(u+2))) now it easy to solve

$$\left(\mathrm{1}\right)\:\int\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{3sin}\:\mathrm{x}−\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}= \\ $$$$\int\:\frac{\mathrm{d}\left(\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}−\mathrm{2}}\:=\:\int\:\frac{\mathrm{du}}{\left(\mathrm{2u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{2}\right)} \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$

Commented by PRITHWISH SEN 2 last updated on 20/May/20

3)put sinx=(√2)t⇒cosxdx=(√2) dt ∫(dt/( (√2)(1+t^2 ))) = (1/( (√2))) tan^(−1) (((sin x)/( (√2))) )+C 4) ∫sec^2 xdx+∫tan^2 x dx = 2∫sec^2 x dx −∫dx = 2tan x−x+C 5)∫[x+ln(e−x)]dx= (x^2 /2)+xln(e−x)+∫(x/(e−x))dx = (x^2 /2)+xln(e−x)−eln(e−x)−x+C

$$\left.\mathrm{3}\right)\mathrm{put}\:\mathrm{sinx}=\sqrt{\mathrm{2}}\mathrm{t}\Rightarrow\mathrm{cosxdx}=\sqrt{\mathrm{2}}\:\mathrm{dt} \\ $$$$\int\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}}\:\right)+\mathrm{C} \\ $$$$\left.\mathrm{4}\right)\:\int\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}+\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\:\mathrm{2}\int\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:−\int\mathrm{dx} \\ $$$$=\:\mathrm{2tan}\:\mathrm{x}−\mathrm{x}+\mathrm{C} \\ $$$$\left.\mathrm{5}\right)\int\left[\mathrm{x}+\mathrm{ln}\left(\mathrm{e}−\mathrm{x}\right)\right]\mathrm{dx}=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{xln}\left(\mathrm{e}−\mathrm{x}\right)+\int\frac{\mathrm{x}}{\mathrm{e}−\mathrm{x}}\mathrm{dx} \\ $$$$=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{xln}\left(\mathrm{e}−\mathrm{x}\right)−\mathrm{eln}\left(\mathrm{e}−\mathrm{x}\right)−\mathrm{x}+\mathrm{C} \\ $$

Answered by Rio Michael last updated on 20/May/20

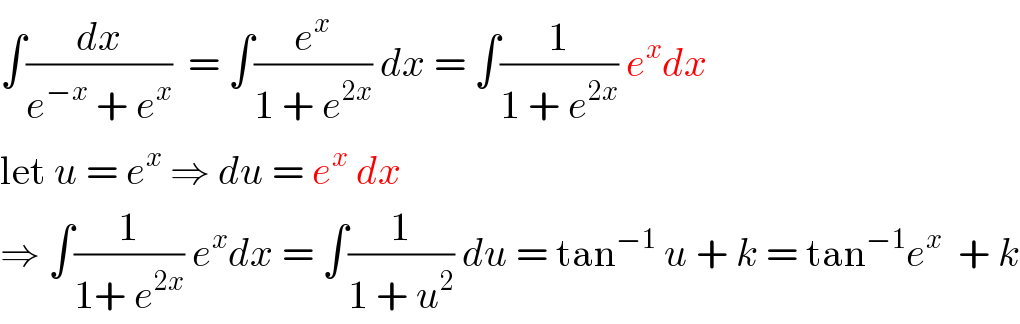
∫(dx/(e^(−x) + e^x )) = ∫(e^x /(1 + e^(2x) )) dx = ∫(1/(1 + e^(2x) )) e^x dx let u = e^x ⇒ du = e^x dx ⇒ ∫(1/(1+ e^(2x) )) e^x dx = ∫(1/(1 + u^2 )) du = tan^(−1) u + k = tan^(−1) e^x + k

$$\int\frac{{dx}}{{e}^{−{x}} \:+\:{e}^{{x}} }\:\:=\:\int\frac{{e}^{{x}} }{\mathrm{1}\:+\:{e}^{\mathrm{2}{x}} }\:{dx}\:=\:\int\frac{\mathrm{1}}{\mathrm{1}\:+\:{e}^{\mathrm{2}{x}} }\:{e}^{{x}} {dx} \\ $$$$\mathrm{let}\:{u}\:=\:{e}^{{x}} \:\Rightarrow\:{du}\:=\:{e}^{{x}} \:{dx} \\ $$$$\Rightarrow\:\int\frac{\mathrm{1}}{\mathrm{1}+\:{e}^{\mathrm{2}{x}} }\:{e}^{{x}} {dx}\:=\:\int\frac{\mathrm{1}}{\mathrm{1}\:+\:{u}^{\mathrm{2}} }\:{du}\:=\:\mathrm{tan}^{−\mathrm{1}} \:{u}\:+\:{k}\:=\:\mathrm{tan}^{−\mathrm{1}} {e}^{{x}} \:\:+\:{k} \\ $$

Answered by i jagooll last updated on 20/May/20

(2) ∫ (e^x /(1+e^(2x) )) dx = ∫ (du/(1+u^2 )) , [ u = e^x ] = tan^(−1) (u) + c = tan^(−1) (e^x ) + c

$$\left(\mathrm{2}\right)\:\int\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:,\:\left[\:\mathrm{u}\:=\:\mathrm{e}^{\mathrm{x}} \:\right] \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\:+\:\mathrm{c}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)\:+\:\mathrm{c}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply