Question-94774

Question Number 94774 by Hamida last updated on 20/May/20

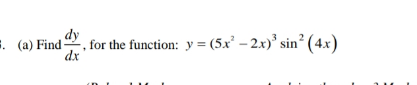
Commented by peter frank last updated on 20/May/20

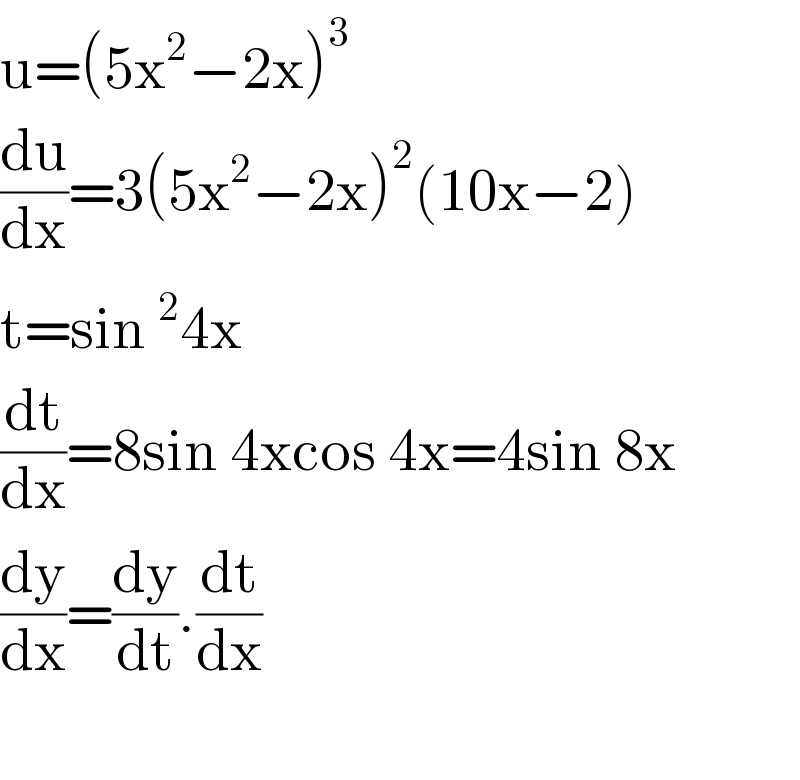
u=(5x^2 −2x)^3 (du/dx)=3(5x^2 −2x)^2 (10x−2) t=sin^2 4x (dt/dx)=8sin 4xcos 4x=4sin 8x (dy/dx)=(dy/dt).(dt/dx)

$$\mathrm{u}=\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{3}} \\ $$$$\frac{\mathrm{du}}{\mathrm{dx}}=\mathrm{3}\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{10x}−\mathrm{2}\right) \\ $$$$\mathrm{t}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{4x} \\ $$$$\frac{\mathrm{dt}}{\mathrm{dx}}=\mathrm{8sin}\:\mathrm{4xcos}\:\mathrm{4x}=\mathrm{4sin}\:\mathrm{8x} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{dy}}{\mathrm{dt}}.\frac{\mathrm{dt}}{\mathrm{dx}} \\ $$$$ \\ $$

Answered by prakash jain last updated on 21/May/20

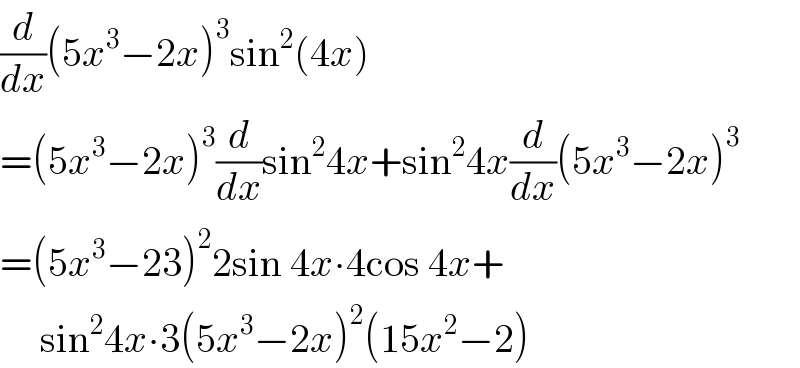
(d/dx)(5x^3 −2x)^3 sin^2 (4x) =(5x^3 −2x)^3 (d/dx)sin^2 4x+sin^2 4x(d/dx)(5x^3 −2x)^3 =(5x^3 −23)^2 2sin 4x∙4cos 4x+ sin^2 4x∙3(5x^3 −2x)^2 (15x^2 −2)

$$\frac{{d}}{{dx}}\left(\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right) \\ $$$$=\left(\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{3}} \frac{{d}}{{dx}}\mathrm{sin}^{\mathrm{2}} \mathrm{4}{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{4}{x}\frac{{d}}{{dx}}\left(\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{5}{x}^{\mathrm{3}} −\mathrm{23}\right)^{\mathrm{2}} \mathrm{2sin}\:\mathrm{4}{x}\centerdot\mathrm{4cos}\:\mathrm{4}{x}+ \\ $$$$\:\:\:\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{4}{x}\centerdot\mathrm{3}\left(\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{2}} \left(\mathrm{15}{x}^{\mathrm{2}} −\mathrm{2}\right) \\ $$

Answered by mathmax by abdo last updated on 21/May/20

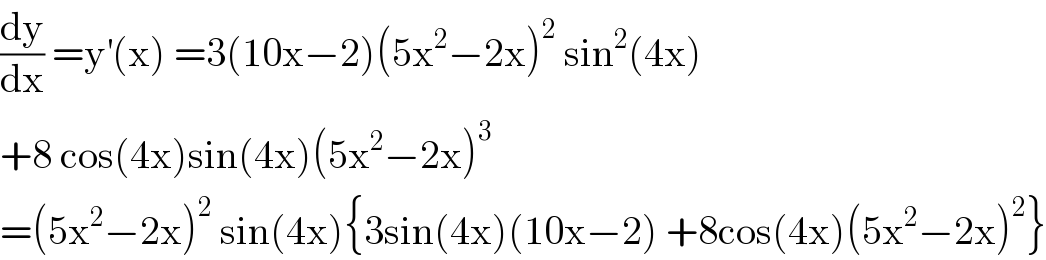
(dy/dx) =y^′ (x) =3(10x−2)(5x^2 −2x)^2 sin^2 (4x) +8 cos(4x)sin(4x)(5x^2 −2x)^3 =(5x^2 −2x)^2 sin(4x){3sin(4x)(10x−2) +8cos(4x)(5x^2 −2x)^2 }

$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\mathrm{y}^{'} \left(\mathrm{x}\right)\:=\mathrm{3}\left(\mathrm{10x}−\mathrm{2}\right)\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{4x}\right) \\ $$$$+\mathrm{8}\:\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}\left(\mathrm{4x}\right)\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{4x}\right)\left\{\mathrm{3sin}\left(\mathrm{4x}\right)\left(\mathrm{10x}−\mathrm{2}\right)\:+\mathrm{8cos}\left(\mathrm{4x}\right)\left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2x}\right)^{\mathrm{2}} \right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply