Question Number 94816 by i jagooll last updated on 21/May/20

Commented by i jagooll last updated on 21/May/20

Commented by i jagooll last updated on 21/May/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Answered by mr W last updated on 21/May/20
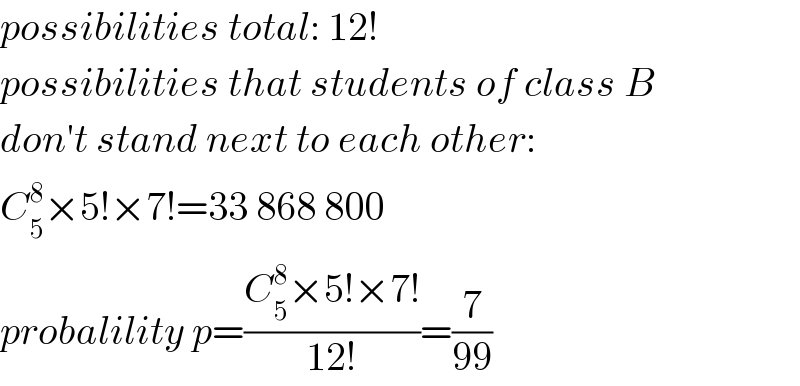
$${possibilities}\:{total}:\:\mathrm{12}! \\ $$$${possibilities}\:{that}\:{students}\:{of}\:{class}\:{B} \\ $$$${don}'{t}\:{stand}\:{next}\:{to}\:{each}\:{other}: \\ $$$${C}_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{5}!×\mathrm{7}!=\mathrm{33}\:\mathrm{868}\:\mathrm{800} \\ $$$${probalility}\:{p}=\frac{{C}_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{5}!×\mathrm{7}!}{\mathrm{12}!}=\frac{\mathrm{7}}{\mathrm{99}} \\ $$
Commented by i jagooll last updated on 21/May/20

$$\mathrm{how}\:\mathrm{get}\:\mathrm{C}_{\mathrm{5}} ^{\mathrm{8}} \:\mathrm{sir}? \\ $$
Commented by mr W last updated on 21/May/20

$${if}\:{we}\:{have}\:\mathrm{5}\:{red}\:{balls}\:{and}\:\mathrm{7}\:{blues} \\ $$$${balls}\:{and}\:{we}\:{place}\:{them}\:{in}\:{a}\:{line} \\ $$$${such}\:{that}\:{no}\:{red}\:{balls}\:{are}\:{next}\:{to} \\ $$$${each}\:{other}.\:{how}\:{many}\:{ways}?\:{certainly} \\ $$$${much}\:{more}\:{than}\:\mathrm{3},\:{i}\:{think}. \\ $$
Commented by i jagooll last updated on 21/May/20

Commented by i jagooll last updated on 21/May/20

$$\mathrm{i}\:\mathrm{got}\:\mathrm{it}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 21/May/20
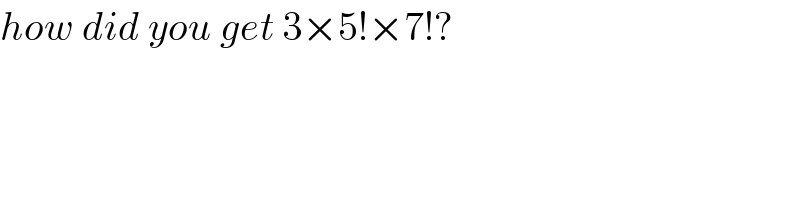
$${how}\:{did}\:{you}\:{get}\:\mathrm{3}×\mathrm{5}!×\mathrm{7}!? \\ $$
Commented by prakash jain last updated on 21/May/20

$$\mathrm{7}\:\mathrm{students}\:\mathrm{provide}\:\mathrm{8}\:\mathrm{possibilities} \\ $$$$\mathrm{for}\:\mathrm{class}\:\mathrm{B}\:\mathrm{student}\:\mathrm{to}\:\mathrm{occupo} \\ $$$$−\mathrm{A}−\mathrm{A}−\mathrm{A}−\mathrm{A}−\mathrm{A}−\mathrm{A}−\mathrm{A}− \\ $$$$−\:\mathrm{are}\:\mathrm{spaces}\:\mathrm{available}\:\mathrm{for}\:\mathrm{class}\:\mathrm{B}. \\ $$
Commented by mr W last updated on 21/May/20

$${how}\:{i}\:{solved}: \\ $$$${students}\:{from}\:{class}\:{B}\:{must}\:{be}\:{separated} \\ $$$${by}\:{at}\:{least}\:{one}\:{student}\:{from}\:{class}\:{A}. \\ $$$${so}\:{we}\:{arrange}\:{at}\:{first}\:{the}\:{students} \\ $$$${from}\:{class}\:{A},\:{there}\:{are}\:\mathrm{7}!\:{ways}. \\ $$$$\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box\boldsymbol{{A}}\Box \\ $$$${now}\:{we}\:{place}\:{the}\:{students}\:{from}\:{class} \\ $$$${B}.\:{they}\:{can}\:{be}\:{placed}\:{in}\:{the}\:{positions} \\ $$$$\Box.\:{from}\:{these}\:\mathrm{8}\:{possible}\:{positions}\:{we} \\ $$$${select}\:\mathrm{5}\:{from}\:{students}\:{of}\:{class}\:{B}, \\ $$$${there}\:{are}\:{C}_{\mathrm{5}} ^{\mathrm{8}} \:{ways}.\:{to}\:{arrange}\:{these}\:\mathrm{5} \\ $$$${students}\:{in}\:{the}\:{selected}\:\mathrm{5}\:{positions} \\ $$$${there}\:{are}\:\mathrm{5}!\:{ways}.\:{therefore}\:{the} \\ $$$${total}\:{possibilities}\:{to}\:{arrange}\:{the} \\ $$$$\mathrm{12}\:{students}\:{such}\:{that}\:{no}\:{students} \\ $$$${from}\:{class}\:{B}\:{are}\:{next}\:{to}\:{each}\:{other} \\ $$$${are}\:\mathrm{7}!×{C}_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{5}!. \\ $$
Commented by i jagooll last updated on 21/May/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{it}\:\mathrm{right} \\ $$
