Question Number 94847 by i jagooll last updated on 21/May/20
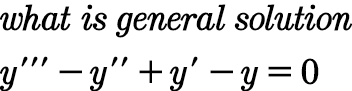
Answered by john santu last updated on 21/May/20
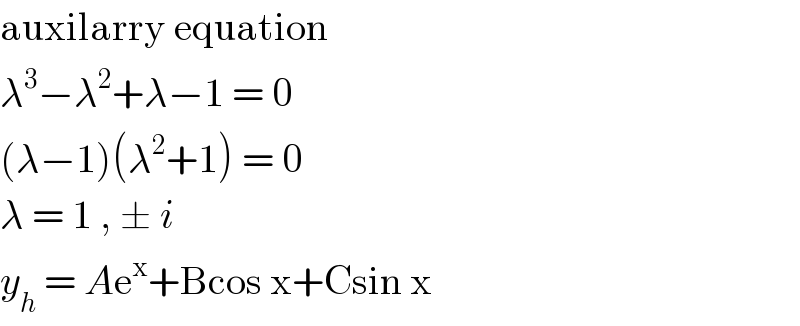
$$\mathrm{auxilarry}\:\mathrm{equation}\: \\ $$$$\lambda^{\mathrm{3}} −\lambda^{\mathrm{2}} +\lambda−\mathrm{1}\:=\:\mathrm{0}\: \\ $$$$\left(\lambda−\mathrm{1}\right)\left(\lambda^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\lambda\:=\:\mathrm{1}\:,\:\pm\:{i}\: \\ $$$${y}_{{h}} \:=\:{A}\mathrm{e}^{\mathrm{x}} +\mathrm{Bcos}\:\mathrm{x}+\mathrm{Csin}\:\mathrm{x}\: \\ $$
Answered by Raxreedoroid last updated on 22/May/20
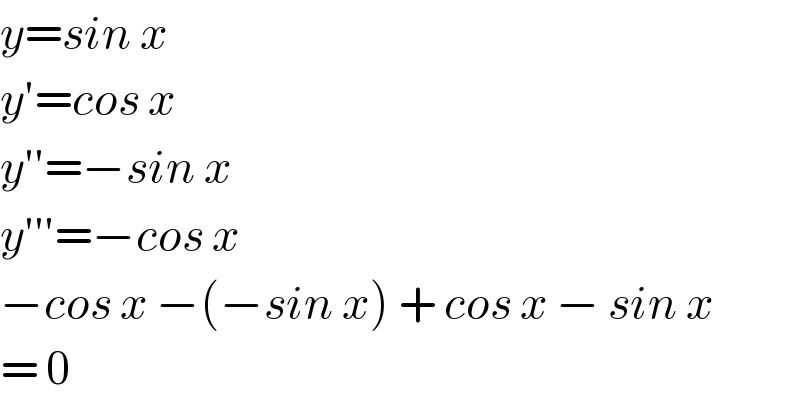
$${y}={sin}\:{x} \\ $$$${y}'={cos}\:{x} \\ $$$${y}''=−{sin}\:{x} \\ $$$${y}'''=−{cos}\:{x} \\ $$$$−{cos}\:{x}\:−\left(−{sin}\:{x}\right)\:+\:{cos}\:{x}\:−\:{sin}\:{x} \\ $$$$=\:\mathrm{0} \\ $$
