Question Number 94868 by O Predador last updated on 21/May/20

Commented by john santu last updated on 21/May/20
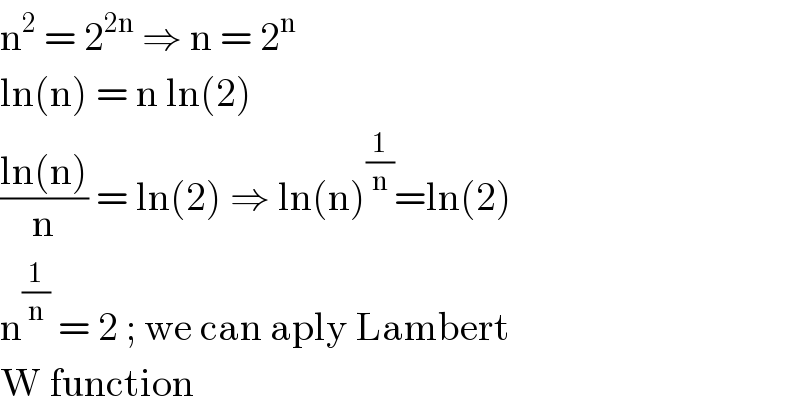
$$\mathrm{n}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{2n}} \:\Rightarrow\:\mathrm{n}\:=\:\mathrm{2}^{\mathrm{n}} \: \\ $$$$\mathrm{ln}\left(\mathrm{n}\right)\:=\:\mathrm{n}\:\mathrm{ln}\left(\mathrm{2}\right)\: \\ $$$$\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}}\:=\:\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{ln}\left(\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\:\mathrm{2}\:;\:\mathrm{we}\:\mathrm{can}\:\mathrm{aply}\:\mathrm{Lambert} \\ $$$$\mathrm{W}\:\mathrm{function}\: \\ $$
Commented by hknkrc46 last updated on 21/May/20
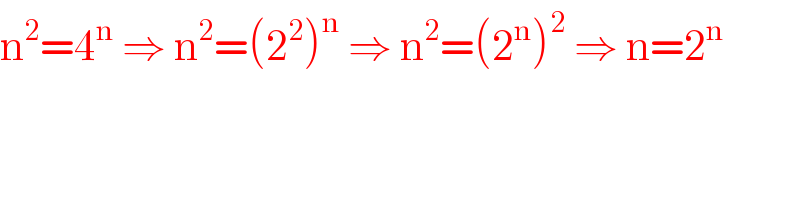
$$\mathrm{n}^{\mathrm{2}} =\mathrm{4}^{\mathrm{n}} \:\Rightarrow\:\mathrm{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{2}} \right)^{\mathrm{n}} \:\Rightarrow\:\mathrm{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{n}} \right)^{\mathrm{2}} \:\Rightarrow\:\mathrm{n}=\mathrm{2}^{\mathrm{n}} \\ $$$$ \\ $$
Commented by O Predador last updated on 21/May/20

$$\: \\ $$$$\:\mathrm{Obrigado}! \\ $$
Commented by mr W last updated on 21/May/20
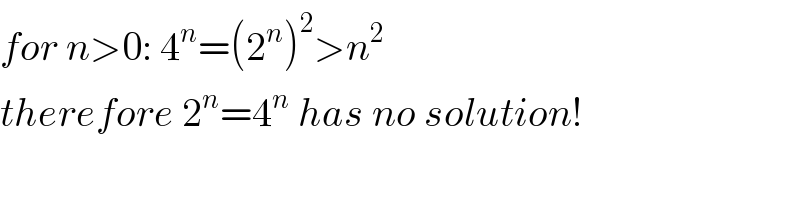
$${for}\:{n}>\mathrm{0}:\:\mathrm{4}^{{n}} =\left(\mathrm{2}^{{n}} \right)^{\mathrm{2}} >{n}^{\mathrm{2}} \\ $$$${therefore}\:\mathrm{2}^{{n}} =\mathrm{4}^{{n}} \:{has}\:{no}\:{solution}! \\ $$
Commented by hknkrc46 last updated on 21/May/20

$$\mathrm{De}\:\mathrm{nada}\:! \\ $$
