Menu Close

Question-94997

Tinku Tara 0 Comments
Pin




Question Number 94997 by i jagooll last updated on 22/May/20
Answered by bobhans last updated on 22/May/20
homogenous solution υ^2 −2υ+2 = 0 υ = 1± i ⇒y_h = Ae^x cos x +Be^x sin x particular integral y_p = ϑ_1 e^x sin x+ϑ_2 e^x cos x y′= ϑ_1 e^x sin x+ϑ_1 e^x cos x+ϑ_2 e^x cos x−ϑ_2 e^x sin x+ (ϑ_1 ′e^x sin x+ϑ_2 ′e^x cos x) set ϑ_1 ′e^x sin x+ϑ_2 ′e^x cos x = 0 y′′= 2e^x (ϑ_1 cos x−ϑ_2 sin x)+(ϑ_1 ′e^x sin x+ϑ_1 ′e^x cos x+ ϑ_2 ′e^x cos x−ϑ_2 ′e^x sin x ) set ϑ_1 ′e^x sin x+ϑ_1 ′e^x cos x+ϑ_2 ′e^x cos x− ϑ_2 ′e^x sin x = e^x (1+sin x) ⇒ϑ_1 = ∫ (cos x+(1/2)sin 2x) dx = sin x−(1/4)cos 2x ⇒ϑ_2 = ∫ (−sin x+((1−cos 2x)/2)) dx ϑ_2 = cos x+(1/2)x−(1/4)sin 2x complete solution y_h +y_p
$$\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\upsilon^{\mathrm{2}} −\mathrm{2}\upsilon+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\upsilon\:=\:\mathrm{1}\pm\:{i}\:\Rightarrow\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}\:+\mathrm{Be}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}\: \\ $$$$\mathrm{particular}\:\mathrm{integral}\: \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\:\vartheta_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}\: \\ $$$$\mathrm{y}'=\:\vartheta_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}+\vartheta_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}−\vartheta_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+ \\ $$$$\left(\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}\right)\: \\ $$$$\mathrm{set}\:\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\mathrm{y}''=\:\mathrm{2e}^{\mathrm{x}} \left(\vartheta_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}−\vartheta_{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\right)+\left(\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}+\right. \\ $$$$\left.\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}−\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}\:\right) \\ $$$$\mathrm{set}\:\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}+\vartheta_{\mathrm{1}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}+\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}− \\ $$$$\vartheta_{\mathrm{2}} '\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{x}} \:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\Rightarrow\vartheta_{\mathrm{1}} \:=\:\int\:\left(\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2x}\right)\:\mathrm{dx}\:=\:\mathrm{sin}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2x} \\ $$$$\Rightarrow\vartheta_{\mathrm{2}} \:=\:\int\:\left(−\mathrm{sin}\:\mathrm{x}+\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}\right)\:\mathrm{dx} \\ $$$$\vartheta_{\mathrm{2}} =\:\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2x}\: \\ $$$$\mathrm{complete}\:\mathrm{solution}\:\mathrm{y}_{\mathrm{h}} +\mathrm{y}_{\mathrm{p}} \: \\ $$
Answered by mathmax by abdo last updated on 23/May/20
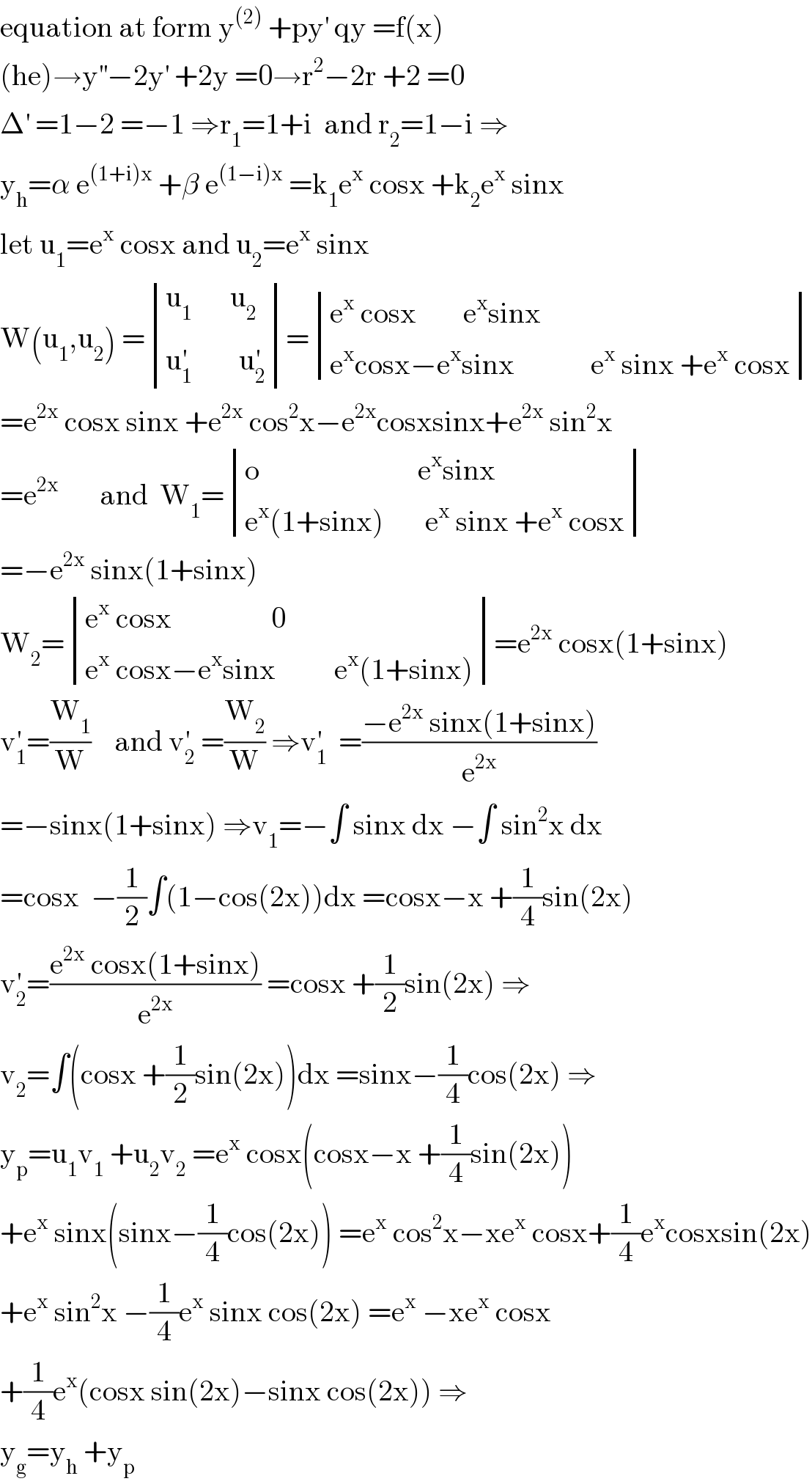
equation at form y^((2)) +py^′ qy =f(x) (he)→y^(′′) −2y^′ +2y =0→r^2 −2r +2 =0 Δ^′ =1−2 =−1 ⇒r_1 =1+i and r_2 =1−i ⇒ y_h =α e^((1+i)x) +β e^((1−i)x) =k_1 e^x cosx +k_2 e^x sinx let u_1 =e^x cosx and u_2 =e^x sinx W(u_1 ,u_2 ) = determinant (((u_(1 ) u_2 )),((u_1 ^′ u_2 ^′ )))= determinant (((e^x cosx e^x sinx)),((e^x cosx−e^x sinx e^x sinx +e^x cosx))) =e^(2x) cosx sinx +e^(2x) cos^2 x−e^(2x) cosxsinx+e^(2x) sin^2 x =e^(2x) and W_1 = determinant (((o e^x sinx)),((e^x (1+sinx) e^x sinx +e^x cosx))) =−e^(2x) sinx(1+sinx) W_2 = determinant (((e^x cosx 0)),((e^x cosx−e^x sinx e^x (1+sinx))))=e^(2x) cosx(1+sinx) v_1 ^′ =(W_1 /W) and v_2 ^′ =(W_2 /W) ⇒v_1 ^′ =((−e^(2x) sinx(1+sinx))/e^(2x) ) =−sinx(1+sinx) ⇒v_1 =−∫ sinx dx −∫ sin^2 x dx =cosx −(1/2)∫(1−cos(2x))dx =cosx−x +(1/4)sin(2x) v_2 ^′ =((e^(2x) cosx(1+sinx))/e^(2x) ) =cosx +(1/2)sin(2x) ⇒ v_2 =∫(cosx +(1/2)sin(2x))dx =sinx−(1/4)cos(2x) ⇒ y_p =u_1 v_1 +u_2 v_2 =e^x cosx(cosx−x +(1/4)sin(2x)) +e^x sinx(sinx−(1/4)cos(2x)) =e^x cos^2 x−xe^x cosx+(1/4)e^x cosxsin(2x) +e^x sin^2 x −(1/4)e^x sinx cos(2x) =e^x −xe^x cosx +(1/4)e^x (cosx sin(2x)−sinx cos(2x)) ⇒ y_g =y_h +y_p
$$\mathrm{equation}\:\mathrm{at}\:\mathrm{form}\:\mathrm{y}^{\left(\mathrm{2}\right)} \:+\mathrm{py}^{'} \:\mathrm{qy}\:=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} −\mathrm{2y}^{'} \:+\mathrm{2y}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2r}\:+\mathrm{2}\:=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{1}−\mathrm{2}\:=−\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{1}+\mathrm{i}\:\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{1}−\mathrm{i}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\alpha\:\mathrm{e}^{\left(\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:+\beta\:\mathrm{e}^{\left(\mathrm{1}−\mathrm{i}\right)\mathrm{x}} \:=\mathrm{k}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}\:+\mathrm{k}_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} \:\mathrm{sinx} \\ $$$$\mathrm{let}\:\mathrm{u}_{\mathrm{1}} =\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}\:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:} \:\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} ^{'} }\end{vmatrix}=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \mathrm{sinx}}\\{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}−\mathrm{e}^{\mathrm{x}} \mathrm{sinx}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx}\:+\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}}\end{vmatrix} \\ $$$$=\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx}\:\mathrm{sinx}\:+\mathrm{e}^{\mathrm{2x}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{e}^{\mathrm{2x}} \mathrm{cosxsinx}+\mathrm{e}^{\mathrm{2x}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x} \\ $$$$=\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\mathrm{and}\:\:\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \mathrm{sinx}}\\{\mathrm{e}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{sinx}\right)\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx}\:+\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}}\end{vmatrix} \\ $$$$=−\mathrm{e}^{\mathrm{2x}} \:\mathrm{sinx}\left(\mathrm{1}+\mathrm{sinx}\right)\:\:\:\: \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}−\mathrm{e}^{\mathrm{x}} \mathrm{sinx}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{sinx}\right)}\end{vmatrix}=\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx}\left(\mathrm{1}+\mathrm{sinx}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} ^{'} =\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\:\:\:\:\mathrm{and}\:\mathrm{v}_{\mathrm{2}} ^{'} \:=\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\:\Rightarrow\mathrm{v}_{\mathrm{1}} ^{'} \:\:=\frac{−\mathrm{e}^{\mathrm{2x}} \:\mathrm{sinx}\left(\mathrm{1}+\mathrm{sinx}\right)}{\mathrm{e}^{\mathrm{2x}} } \\ $$$$=−\mathrm{sinx}\left(\mathrm{1}+\mathrm{sinx}\right)\:\Rightarrow\mathrm{v}_{\mathrm{1}} =−\int\:\mathrm{sinx}\:\mathrm{dx}\:−\int\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\mathrm{cosx}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}\:=\mathrm{cosx}−\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{v}_{\mathrm{2}} ^{'} =\frac{\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx}\left(\mathrm{1}+\mathrm{sinx}\right)}{\mathrm{e}^{\mathrm{2x}} }\:=\mathrm{cosx}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\left(\mathrm{cosx}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\right)\mathrm{dx}\:=\mathrm{sinx}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:=\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}\left(\mathrm{cosx}−\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2x}\right)\right) \\ $$$$+\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx}\left(\mathrm{sinx}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\:=\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{xe}^{\mathrm{x}} \:\mathrm{cosx}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{x}} \mathrm{cosxsin}\left(\mathrm{2x}\right) \\ $$$$+\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx}\:\mathrm{cos}\left(\mathrm{2x}\right)\:=\mathrm{e}^{\mathrm{x}} \:−\mathrm{xe}^{\mathrm{x}} \:\mathrm{cosx}\: \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}\:\mathrm{sin}\left(\mathrm{2x}\right)−\mathrm{sinx}\:\mathrm{cos}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{g}} =\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *