Question Number 95121 by i jagooll last updated on 23/May/20
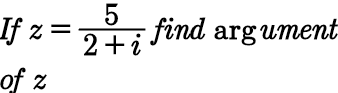
Commented by bobhans last updated on 23/May/20
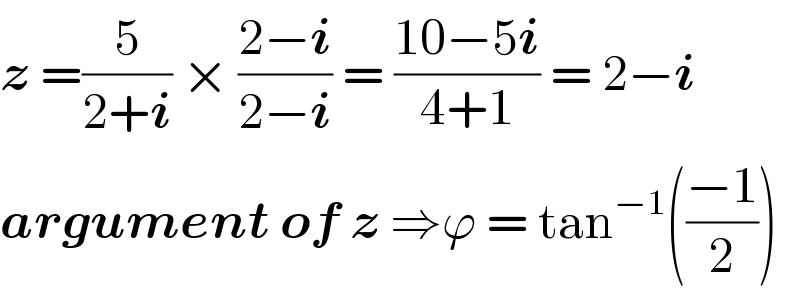
$$\boldsymbol{{z}}\:=\frac{\mathrm{5}}{\mathrm{2}+\boldsymbol{{i}}}\:×\:\frac{\mathrm{2}−\boldsymbol{{i}}}{\mathrm{2}−\boldsymbol{{i}}}\:=\:\frac{\mathrm{10}−\mathrm{5}\boldsymbol{{i}}}{\mathrm{4}+\mathrm{1}}\:=\:\mathrm{2}−\boldsymbol{{i}}\: \\ $$$$\boldsymbol{{argument}}\:\boldsymbol{{of}}\:\boldsymbol{{z}}\:\Rightarrow\varphi\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\: \\ $$
Answered by mathmax by abdo last updated on 24/May/20
![z =(5/(2+i)) we have 2+i =(√5)((2/( (√5))) +(i/( (√5)))) =(√5)(cosθ +isinθ) ⇒ r =(√5) and θ =arctan((1/2)) ⇒z =(5/( (√5)e^(iarctan((1/2))) )) =(√5)e^(−iarctan((1/2)) ) ⇒ arg(z)≡arctan(−(1/2))[2π]](https://www.tinkutara.com/question/Q95210.png)
$$\mathrm{z}\:=\frac{\mathrm{5}}{\mathrm{2}+\mathrm{i}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{2}+\mathrm{i}\:=\sqrt{\mathrm{5}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:+\frac{\mathrm{i}}{\:\sqrt{\mathrm{5}}}\right)\:=\sqrt{\mathrm{5}}\left(\mathrm{cos}\theta\:+\mathrm{isin}\theta\right)\:\Rightarrow \\ $$$$\mathrm{r}\:=\sqrt{\mathrm{5}}\:\mathrm{and}\:\theta\:=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow\mathrm{z}\:=\frac{\mathrm{5}}{\:\sqrt{\mathrm{5}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} }\:=\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:} \:\Rightarrow \\ $$$$\mathrm{arg}\left(\mathrm{z}\right)\equiv\mathrm{arctan}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\mathrm{2}\pi\right] \\ $$
