Question Number 95177 by mr W last updated on 23/May/20
Commented by mr W last updated on 23/May/20

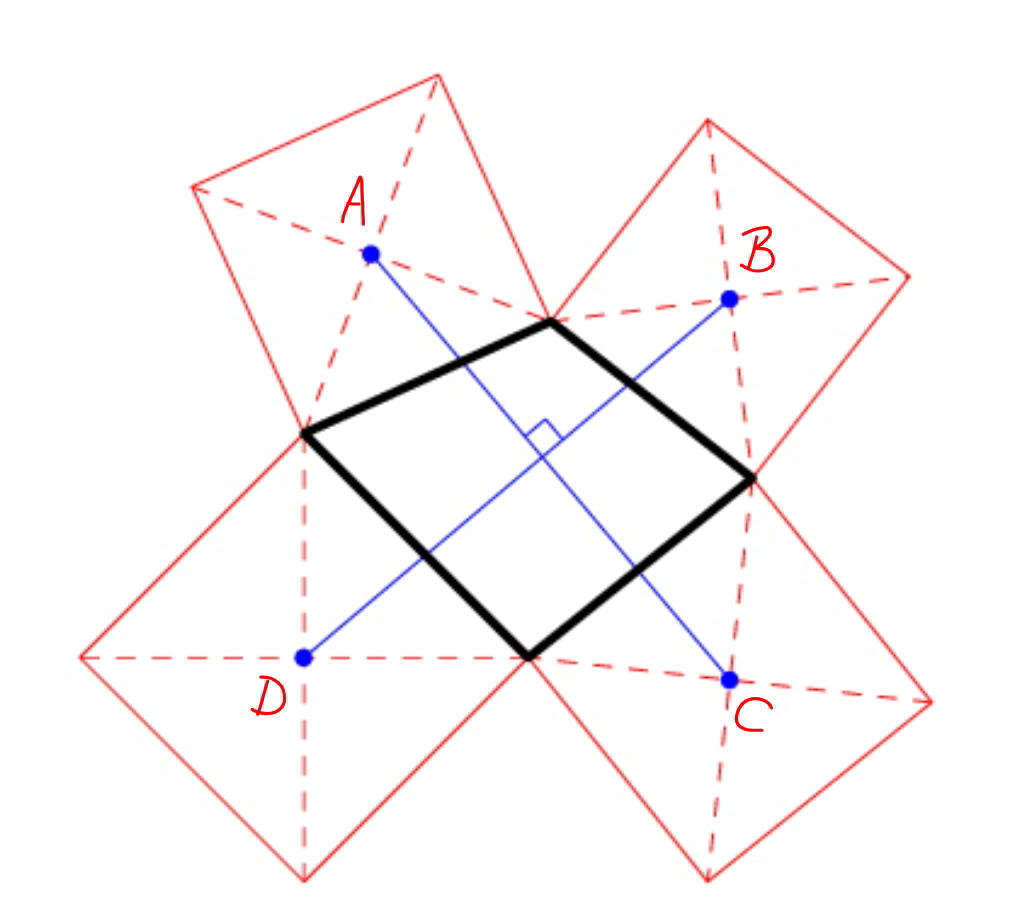
$${A},{B},{C},{D}\:{are}\:{centers}\:{of}\:{the}\:{squares}. \\ $$$${Prove}\:{that}\:{AC}={BD}\:{and}\:{AC}\bot{BD}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 24/May/20

$$\mathrm{sir}\:\mathrm{I}\:\mathrm{have}\:\mathrm{a}\:\mathrm{sol}^{\mathrm{n}} \:\mathrm{with}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\left(\mathrm{though}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{mine}\:\right). \\ $$
Commented by mr W last updated on 24/May/20
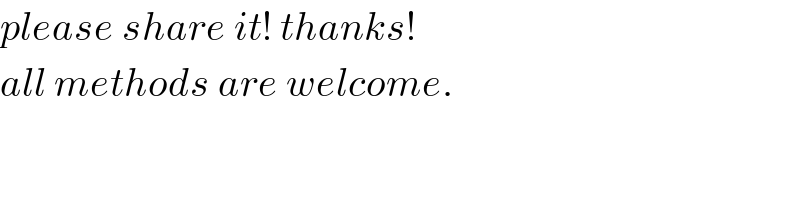
$${please}\:{share}\:{it}!\:{thanks}! \\ $$$${all}\:{methods}\:{are}\:{welcome}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 24/May/20
$$\mathrm{OK}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{it}\:\mathrm{later} \\ $$
Commented by PRITHWISH SEN 2 last updated on 24/May/20

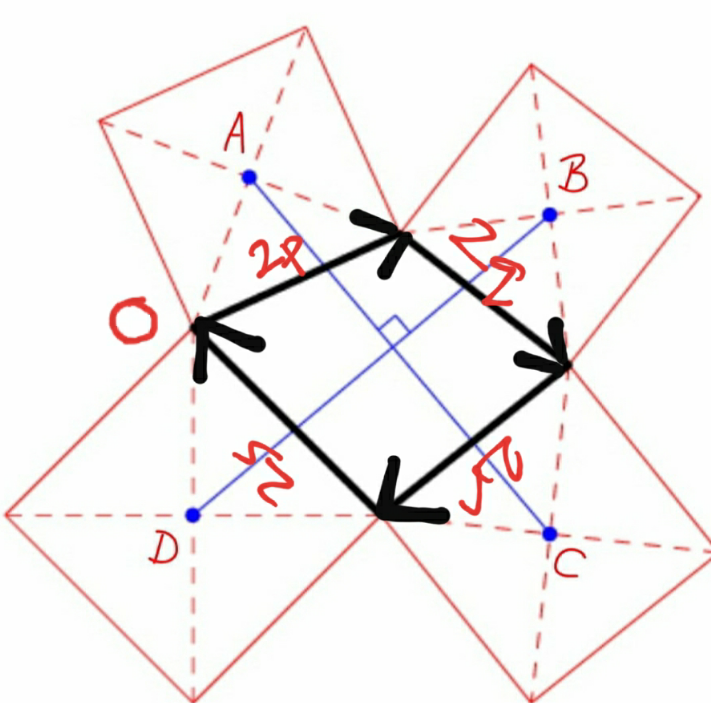
$$\mathrm{let}\:\mathrm{2p},\mathrm{2q},\mathrm{2r}\:\&\mathrm{2s}\:\mathrm{are}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{numbers}\: \\ $$$$\mathrm{represents}\:\mathrm{the}\:\mathrm{four}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadrilateral} \\ $$$$\therefore\:\mathrm{p}+\mathrm{q}+\mathrm{r}+\mathrm{s}=\mathrm{0} \\ $$$$\mathrm{now}\:\:\mathrm{A}\:=\:\mathrm{p}+\boldsymbol{\mathrm{i}}\mathrm{p}\:\:=\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\mathrm{p} \\ $$$$\:\:\mathrm{B}=\:\mathrm{2p}+\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\mathrm{q}\:\:\mathrm{C}=\mathrm{2p}+\mathrm{2q}+\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\mathrm{r} \\ $$$$\mathrm{D}=\:\mathrm{2p}+\mathrm{2q}+\mathrm{2r}+\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\mathrm{s} \\ $$$$\mathrm{AC}=\mathrm{p}+\mathrm{2q}+\mathrm{r}+\boldsymbol{\mathrm{i}}\left(\mathrm{r}−\mathrm{p}\right) \\ $$$$\mathrm{BD}=\mathrm{D}−\mathrm{B}=\mathrm{q}+\mathrm{2r}+\mathrm{s}+\boldsymbol{\mathrm{i}}\left(\mathrm{s}−\mathrm{q}\right) \\ $$$$\mathrm{BD}+\boldsymbol{\mathrm{i}}\mathrm{AC}=\left(\mathrm{p}+\mathrm{q}+\mathrm{r}+\mathrm{s}\right)+\boldsymbol{\mathrm{i}}\left(\mathrm{p}+\mathrm{q}+\mathrm{r}+\mathrm{s}\right)=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{\mathrm{i}}\mathrm{BD}=\mathrm{AC}\Rightarrow\mathrm{BD}=\mathrm{AC}\:\&\:\mathrm{AC}\bot\mathrm{BD} \\ $$
Commented by PRITHWISH SEN 2 last updated on 24/May/20
Commented by mr W last updated on 24/May/20

$${thanks}\:{sir}! \\ $$
