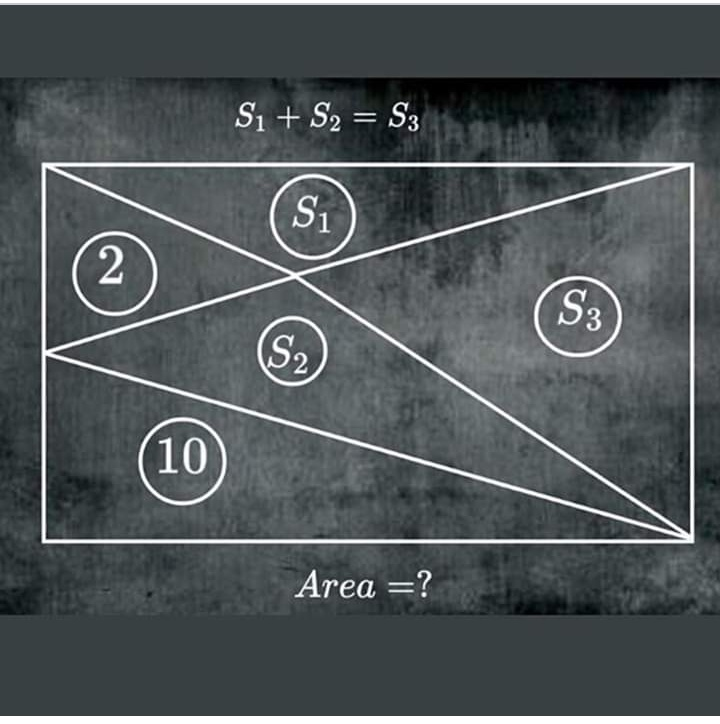
Question Number 95246 by Crabby89p13 last updated on 24/May/20
Answered by mr W last updated on 24/May/20
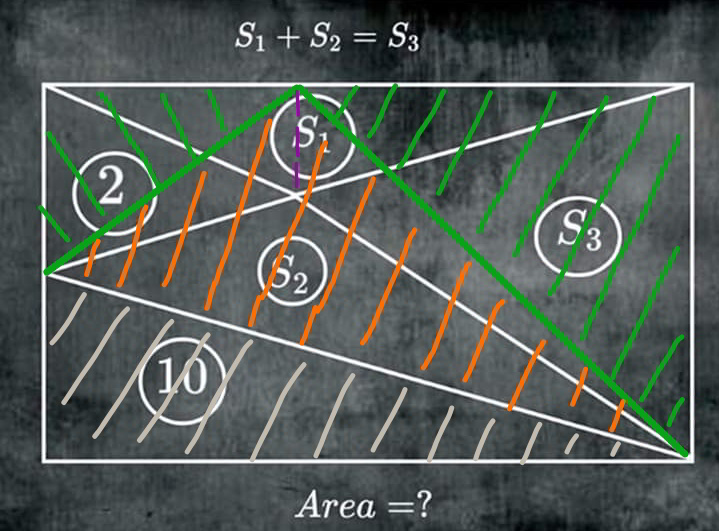
Commented by mr W last updated on 24/May/20
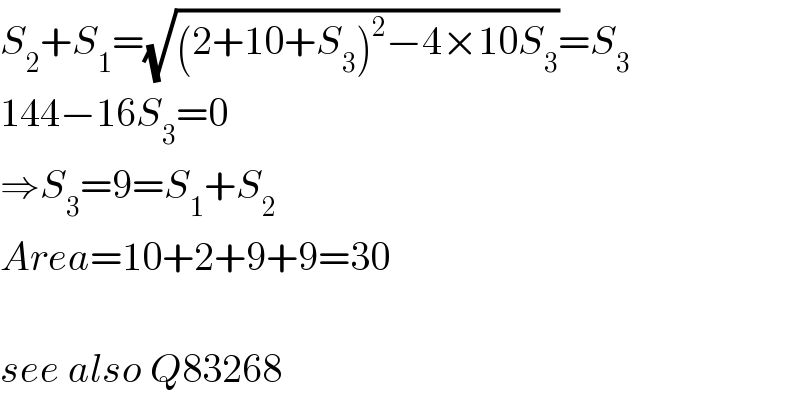
$${S}_{\mathrm{2}} +{S}_{\mathrm{1}} =\sqrt{\left(\mathrm{2}+\mathrm{10}+{S}_{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{4}×\mathrm{10}{S}_{\mathrm{3}} }={S}_{\mathrm{3}} \\ $$$$\mathrm{144}−\mathrm{16}{S}_{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow{S}_{\mathrm{3}} =\mathrm{9}={S}_{\mathrm{1}} +{S}_{\mathrm{2}} \\ $$$${Area}=\mathrm{10}+\mathrm{2}+\mathrm{9}+\mathrm{9}=\mathrm{30} \\ $$$$ \\ $$$${see}\:{also}\:{Q}\mathrm{83268} \\ $$
Commented by mr W last updated on 24/May/20
$${sorry}\:{sir}!\:{i}\:{should}\:{have}\:{had}\:{to}\:{wait} \\ $$$${for}\:{your}\:{solution}.\:{i}\:{am}\:{also}\:{interested} \\ $$$${what}\:{your}\:{path}\:{is}. \\ $$
Commented by Farruxjano last updated on 24/May/20
$$\left.\boldsymbol{{Great}}\:\boldsymbol{{solution}}!!!\:\::\right) \\ $$
Commented by Crabby89p13 last updated on 24/May/20
$${thank}\:{you}\:{so}\:{much} \\ $$
Commented by Farruxjano last updated on 24/May/20

$$\boldsymbol{{ok}}\:\boldsymbol{{i}}'\boldsymbol{{ll}}\:\boldsymbol{{send}}\:\boldsymbol{{it}} \\ $$
Commented by Farruxjano last updated on 24/May/20

$$\boldsymbol{{Please}},\:\boldsymbol{{help}}\:\boldsymbol{{me}}\:\boldsymbol{{I}}\:\boldsymbol{{can}}'\boldsymbol{{t}}\:\boldsymbol{{send}}\:\boldsymbol{{an}}\:\boldsymbol{{image}} \\ $$$$\left(\boldsymbol{{a}}\:\boldsymbol{{picture}}\right) \\ $$
Commented by Farruxjano last updated on 24/May/20

$$\boldsymbol{{Help}}!!!!!!!!!!! \\ $$
Commented by i jagooll last updated on 24/May/20
$$\mathrm{your}\:\mathrm{must}\:\mathrm{be}\:\mathrm{crop}\:\mathrm{the}\:\mathrm{image} \\ $$
Commented by mr W last updated on 24/May/20

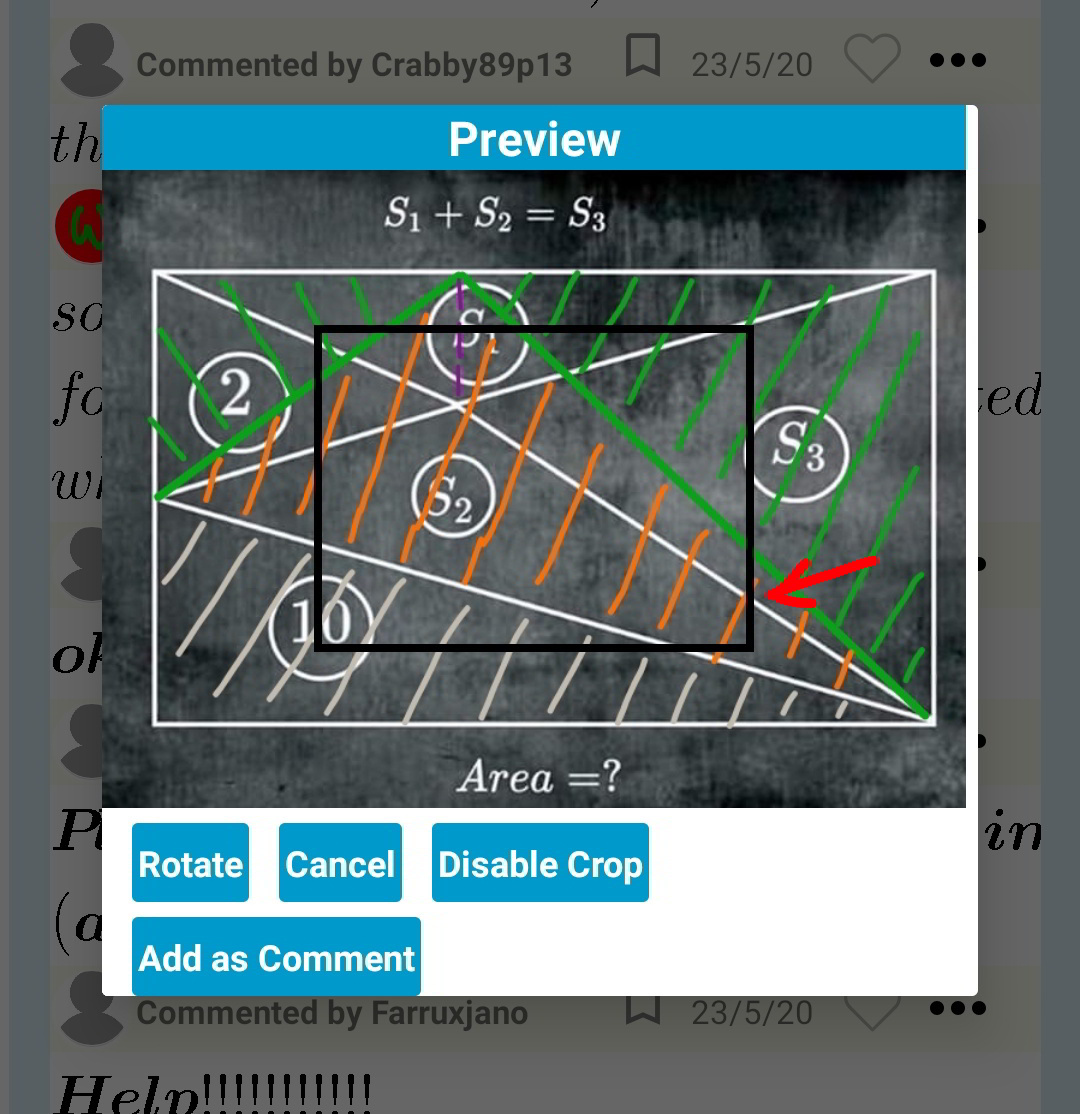
$${This}\:{is}\:{how}\:{to}\:{input}\:{an}\:{image}\:{as} \\ $$$${question},\:{as}\:{answer}\:{or}\:{as}\:{comment} \\ $$$$ \\ $$$${if}\:{you}\:{want}\:{to}\:{input}\:{an}\:{image}\:{as} \\ $$$${a}\:{new}\:{question},\:{just}\:{click}\:{on}\:{the} \\ $$$${picture}\:{icon}\:{in}\:{the}\:{command}\:{line} \\ $$$${on}\:{the}\:{top}\:{of}\:{the}\:{screen}. \\ $$$$ \\ $$$${if}\:{you}\:{want}\:{to}\:{input}\:{an}\:{image}\:{as} \\ $$$${answer}\:{or}\:{comment}\:{to}\:{an}\:{existing} \\ $$$${question},\:{click}\:{on}\:{the}\:\bullet\bullet\bullet\:{icon}\:{on} \\ $$$${the}\:{title}\:{bar}\:{of}\:{the}\:{post}\:{you}\:{want}\:{to} \\ $$$${answer},\:{then}\:{select}\:“{attach}\:{image}''. \\ $$$${then}\:{browse}\:{to}\:{the}\:{place}\:{where}\:{your} \\ $$$${image}\:{is}\:{saved}\:{and}\:{select}\:{the}\:{image}. \\ $$$${then}\:{you}\:{see}\:{following}\:{window}: \\ $$
Commented by mr W last updated on 24/May/20
Commented by mr W last updated on 24/May/20

$${if}\:{you}\:{just}\:{want}\:{to}\:{input}\:{a}\:{part}\:{of} \\ $$$${your}\:{image},\:{then}\:{crop}\:{the}\:{image}\:{by} \\ $$$${moving}\:{and}\:{sizing}\:{the}\:{black}\:{frame}. \\ $$$${only}\:{the}\:{part}\:{within}\:{the}\:{black}\:{frame} \\ $$$${will}\:{be}\:{inputed}.\:{if}\:{your}\:{image}\:{has} \\ $$$${already}\:{the}\:{proper}\:{size},\:{then}\:{you} \\ $$$${don}'{t}\:{need}\:{to}\:{crop}\:{it},\:{in}\:{this}\:{case}\:{you} \\ $$$${can}\:{click}\:{on}\:{the}\:“{disable}\:{crop}''\:{button}, \\ $$$${then}\:{the}\:{whole}\:{image}\:{will}\:{be}\:{inputed}. \\ $$$${certainly}\:{you}\:{can}\:{also}\:{rotate}\:{your} \\ $$$${image}\:{in}\:{case}\:{of}\:{need}.\:{finally}\:{click} \\ $$$${on}\:{the}\:{button}\:“{add}\:{as}\:{comment}''\:{or} \\ $$$$“{add}\:{as}\:{answer}''. \\ $$$${that}'{s}\:{all}. \\ $$
Commented by Farruxjano last updated on 24/May/20
$$\boldsymbol{{Oh}},\:\boldsymbol{{you}}'\boldsymbol{{ve}}\:\boldsymbol{{greatly}}\:\boldsymbol{{helped}}\:\boldsymbol{{me}}!\:\boldsymbol{{Thanks}}! \\ $$
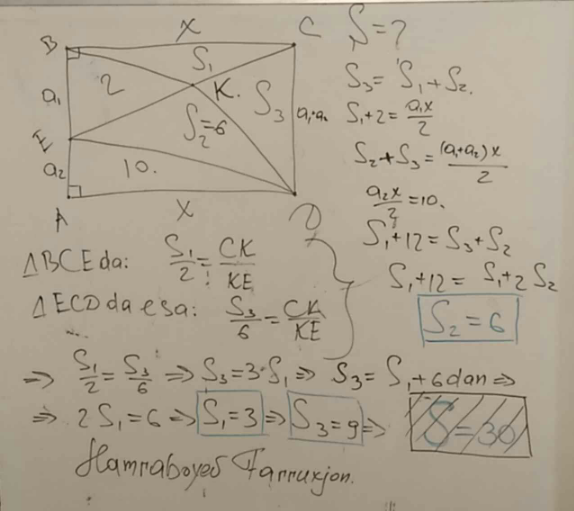
Answered by Farruxjano last updated on 24/May/20
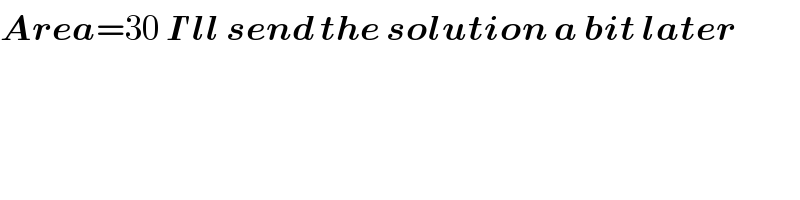
$$\boldsymbol{{Area}}=\mathrm{30}\:\boldsymbol{{I}}'\boldsymbol{{ll}}\:\boldsymbol{{send}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}\:\boldsymbol{{a}}\:\boldsymbol{{bit}}\:\boldsymbol{{later}} \\ $$
Commented by Crabby89p13 last updated on 24/May/20

$${Ok}.. \\ $$
Answered by Farruxjano last updated on 24/May/20
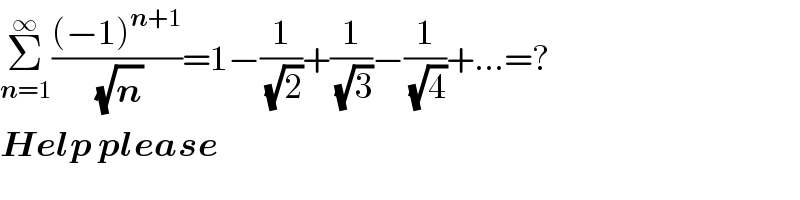
$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} }{\:\sqrt{\boldsymbol{{n}}}}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}+…=? \\ $$$$\boldsymbol{{Help}}\:\boldsymbol{{please}} \\ $$
Commented by mr W last updated on 24/May/20

$${if}\:{you}\:{want}\:{to}\:{introduce}\:{a}\:{new}\:{topic} \\ $$$${or}\:{have}\:{an}\:{other}\:{question},\:{please}\: \\ $$$${open}\:{a}\:{new}\:{thread}.\:{don}'{t}\:{put}\:{it}\:{into} \\ $$$${an}\:{other}\:{existing}\:{thread}\:\left({like}\:{here}\right) \\ $$$${which}\:{has}\:{nothing}\:{to}\:{do}\:{with}\:{your} \\ $$$${topic}. \\ $$$${to}\:{open}\:{a}\:{new}\:{thread}\:{just}\:{click}\:{on} \\ $$$${the}\:“+''\:{icon}\:{on}\:{the}\:{command}\:{line} \\ $$$${on}\:{the}\:{top}\:{of}\:{screen},\:{or}\:{on}\:{the}\:{picture} \\ $$$${icon}\:{if}\:{you}\:{want}\:{to}\:{input}\:{a}\:{picture} \\ $$$${as}\:{new}\:{question}. \\ $$$${i}\:{have}\:{made}\:{big}\:{efforts}\:{to}\:{make} \\ $$$${all}\:{these}\:“{how}\:{to}\:{do}''{s}\:{for}\:{you},\:{please}\: \\ $$$${use}\:{them}! \\ $$
Answered by Farruxjano last updated on 24/May/20