Menu Close

Question-95464

Tinku Tara 0 Comments
Pin




Question Number 95464 by i jagooll last updated on 25/May/20
Commented by i jagooll last updated on 25/May/20
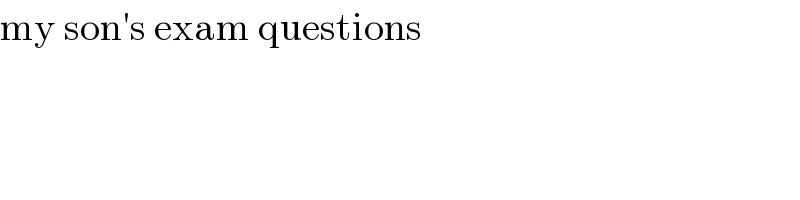
my son′s exam questions
$$\mathrm{my}\:\mathrm{son}'\mathrm{s}\:\mathrm{exam}\:\mathrm{questions} \\ $$
Commented by john santu last updated on 25/May/20
Commented by john santu last updated on 25/May/20
area of square = 16 cm^2 area of ΔPBQ = (1/4)×16 cm^2 = 4 cm^2 BT : PS = 1:2 ⇒BT = 2 cm ((area of ΔCBT)/(area of ΔPCS)) = (a/(4a)) =(1/4) in ΔPBT ; PC :CB = 1:2 ((area of ΔCBT)/(area of ΔPCT)) = (a/(2a)) ⇒6a = 4 ⇒a = (2/3) . area of shaded region = 2a = (4/3)
$$\mathrm{area}\:\mathrm{of}\:\mathrm{square}\:=\:\mathrm{16}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{PBQ}\:=\:\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{16}\:\mathrm{cm}^{\mathrm{2}} \:\:=\:\mathrm{4}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{BT}\::\:\mathrm{PS}\:=\:\mathrm{1}:\mathrm{2}\:\Rightarrow\mathrm{BT}\:=\:\mathrm{2}\:\mathrm{cm} \\ $$$$\frac{\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{CBT}}{\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{PCS}}\:=\:\frac{\mathrm{a}}{\mathrm{4a}}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{in}\:\Delta\mathrm{PBT}\:;\:\mathrm{PC}\::\mathrm{CB}\:=\:\mathrm{1}:\mathrm{2}\: \\ $$$$\frac{\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{CBT}}{\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{PCT}}\:=\:\frac{\mathrm{a}}{\mathrm{2a}}\: \\ $$$$\Rightarrow\mathrm{6a}\:=\:\mathrm{4}\:\Rightarrow\mathrm{a}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{region}\:=\:\mathrm{2a}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by mr W last updated on 25/May/20
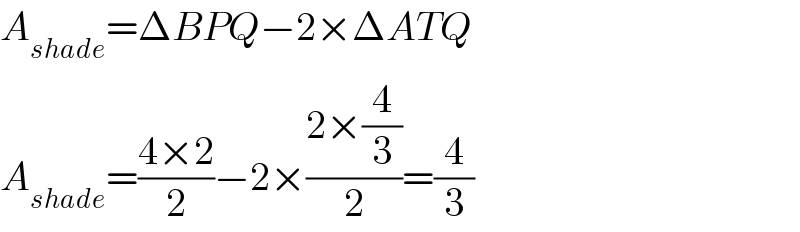
A_(shade) =ΔBPQ−2×ΔATQ A_(shade) =((4×2)/2)−2×((2×(4/3))/2)=(4/3)
$${A}_{{shade}} =\Delta{BPQ}−\mathrm{2}×\Delta{ATQ} \\ $$$${A}_{{shade}} =\frac{\mathrm{4}×\mathrm{2}}{\mathrm{2}}−\mathrm{2}×\frac{\mathrm{2}×\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 25/May/20
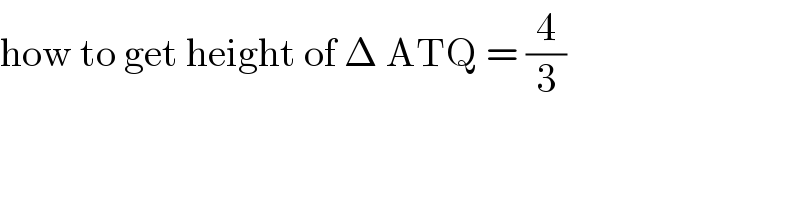
how to get height of Δ ATQ = (4/3)
$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{height}\:\mathrm{of}\:\Delta\:\mathrm{ATQ}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by i jagooll last updated on 25/May/20
thank you both
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
Commented by mr W last updated on 25/May/20
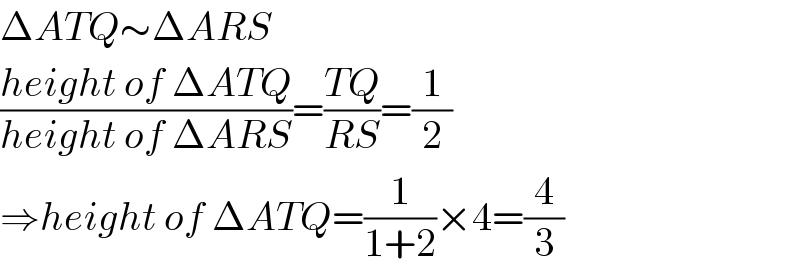
ΔATQ∼ΔARS ((height of ΔATQ)/(height of ΔARS))=((TQ)/(RS))=(1/2) ⇒height of ΔATQ=(1/(1+2))×4=(4/3)
$$\Delta{ATQ}\sim\Delta{ARS} \\ $$$$\frac{{height}\:{of}\:\Delta{ATQ}}{{height}\:{of}\:\Delta{ARS}}=\frac{{TQ}}{{RS}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{height}\:{of}\:\Delta{ATQ}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}}×\mathrm{4}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 25/May/20
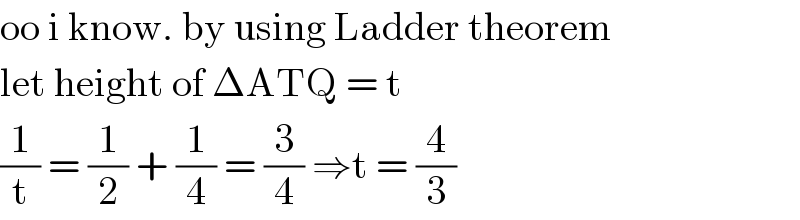
oo i know. by using Ladder theorem let height of ΔATQ = t (1/t) = (1/2) + (1/4) = (3/4) ⇒t = (4/3)
$$\mathrm{oo}\:\mathrm{i}\:\mathrm{know}.\:\mathrm{by}\:\mathrm{using}\:\mathrm{Ladder}\:\mathrm{theorem} \\ $$$$\mathrm{let}\:\mathrm{height}\:\mathrm{of}\:\Delta\mathrm{ATQ}\:=\:\mathrm{t}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{t}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\mathrm{t}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *