Question Number 95560 by I want to learn more last updated on 26/May/20

Commented by i jagooll last updated on 26/May/20
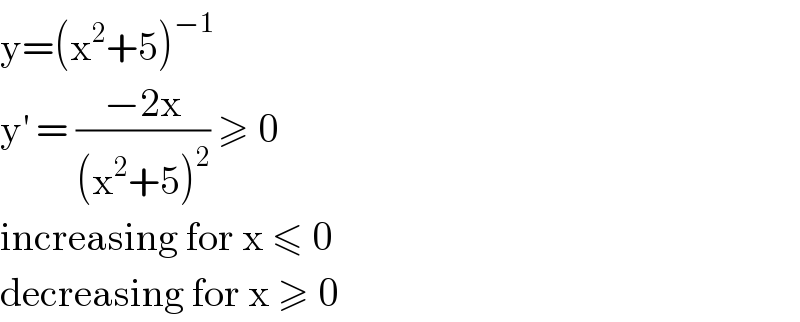
$$\mathrm{y}=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5}\right)^{−\mathrm{1}} \: \\ $$$$\mathrm{y}^{'} \:=\:\frac{−\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{2}} }\:\geqslant\:\mathrm{0}\: \\ $$$$\mathrm{increasing}\:\mathrm{for}\:\mathrm{x}\:\leqslant\:\mathrm{0}\: \\ $$$$\mathrm{decreasing}\:\mathrm{for}\:\mathrm{x}\:\geqslant\:\mathrm{0}\: \\ $$
Answered by mr W last updated on 26/May/20

$${y}'=−\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{2}} } \\ $$$${y}\:{increases}\:{or}\:{decreases}\:{most}\:{rapidly} \\ $$$${means}\:{y}'\:{is}\:{maximum}\:{or}\:{minimum}, \\ $$$${that}\:{means}\:{again}\:{y}''=\mathrm{0}. \\ $$$${y}''=−\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{2}} }+\frac{\mathrm{4}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{5} \\ $$$$\Rightarrow{x}=\pm\sqrt{\mathrm{5}} \\ $$$${at}\:{x}=−\sqrt{\mathrm{5}}:\:{y}'>\mathrm{0},\:{y}\:{increases}\:{most}\:{rapidly}. \\ $$$${at}\:{x}=\sqrt{\mathrm{5}}:\:{y}'<\mathrm{0},\:{y}\:{decreases}\:{most}\:{rapidly}. \\ $$
Commented by I want to learn more last updated on 26/May/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by peter frank last updated on 26/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
