Question Number 95608 by bobhans last updated on 26/May/20
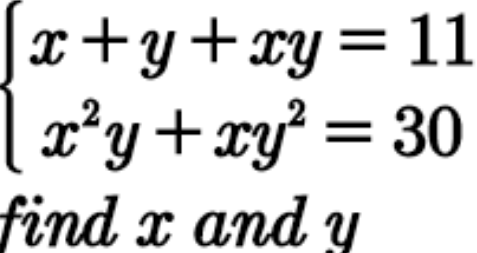
Commented by john santu last updated on 26/May/20
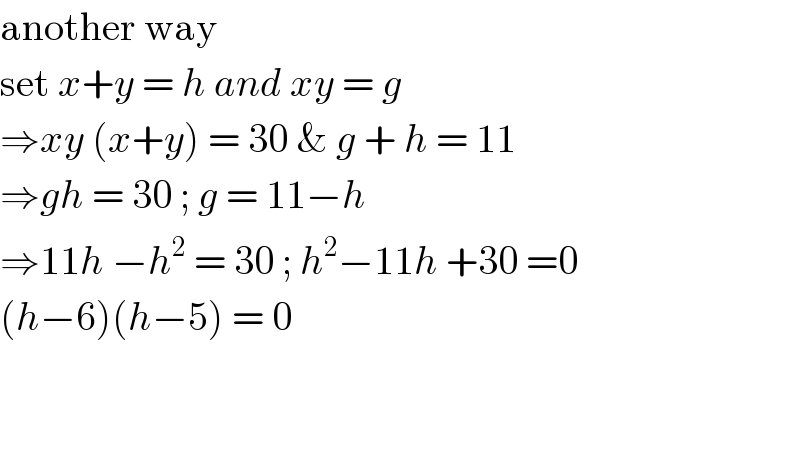
$$\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{set}\:{x}+{y}\:=\:{h}\:{and}\:{xy}\:=\:{g} \\ $$$$\Rightarrow{xy}\:\left({x}+{y}\right)\:=\:\mathrm{30}\:\&\:{g}\:+\:{h}\:=\:\mathrm{11} \\ $$$$\Rightarrow{gh}\:=\:\mathrm{30}\:;\:{g}\:=\:\mathrm{11}−{h} \\ $$$$\Rightarrow\mathrm{11}{h}\:−{h}^{\mathrm{2}} \:=\:\mathrm{30}\:;\:{h}^{\mathrm{2}} −\mathrm{11}{h}\:+\mathrm{30}\:=\mathrm{0} \\ $$$$\left({h}−\mathrm{6}\right)\left({h}−\mathrm{5}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by bobhans last updated on 26/May/20
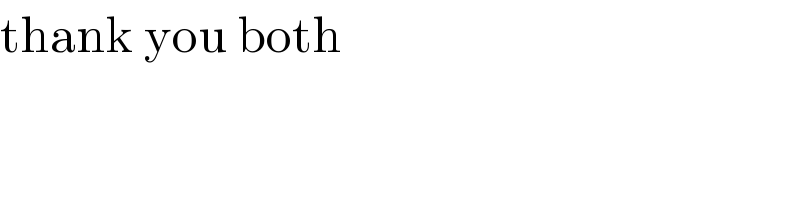
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
Answered by john santu last updated on 26/May/20
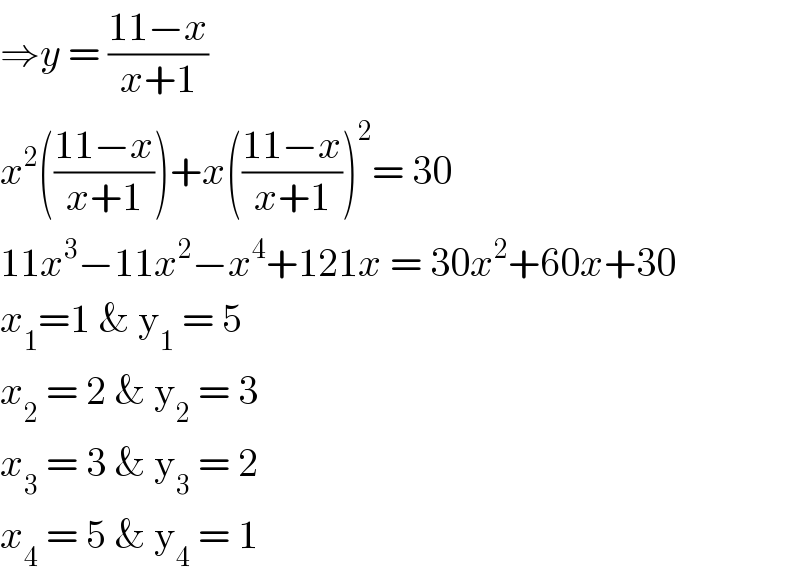
$$\Rightarrow{y}\:=\:\frac{\mathrm{11}−{x}}{{x}+\mathrm{1}} \\ $$$${x}^{\mathrm{2}} \left(\frac{\mathrm{11}−{x}}{{x}+\mathrm{1}}\right)+{x}\left(\frac{\mathrm{11}−{x}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{30} \\ $$$$\mathrm{11}{x}^{\mathrm{3}} −\mathrm{11}{x}^{\mathrm{2}} −{x}^{\mathrm{4}} +\mathrm{121}{x}\:=\:\mathrm{30}{x}^{\mathrm{2}} +\mathrm{60}{x}+\mathrm{30} \\ $$$${x}_{\mathrm{1}} =\mathrm{1}\:\&\:\mathrm{y}_{\mathrm{1}} \:=\:\mathrm{5} \\ $$$${x}_{\mathrm{2}} \:=\:\mathrm{2}\:\&\:\mathrm{y}_{\mathrm{2}} \:=\:\mathrm{3} \\ $$$${x}_{\mathrm{3}} \:=\:\mathrm{3}\:\&\:\mathrm{y}_{\mathrm{3}} \:=\:\mathrm{2} \\ $$$${x}_{\mathrm{4}} \:=\:\mathrm{5}\:\&\:\mathrm{y}_{\mathrm{4}} \:=\:\mathrm{1}\: \\ $$
Answered by MJS last updated on 26/May/20
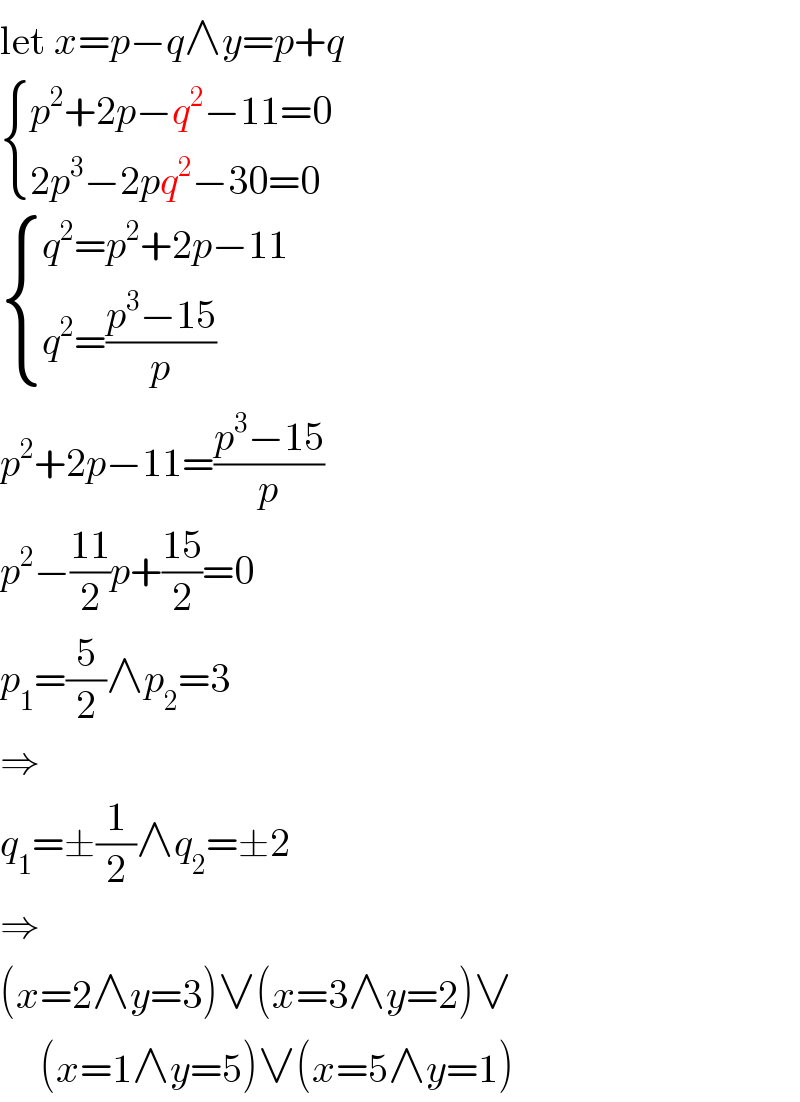
$$\mathrm{let}\:{x}={p}−{q}\wedge{y}={p}+{q} \\ $$$$\begin{cases}{{p}^{\mathrm{2}} +\mathrm{2}{p}−{q}^{\mathrm{2}} −\mathrm{11}=\mathrm{0}}\\{\mathrm{2}{p}^{\mathrm{3}} −\mathrm{2}{pq}^{\mathrm{2}} −\mathrm{30}=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{{q}^{\mathrm{2}} ={p}^{\mathrm{2}} +\mathrm{2}{p}−\mathrm{11}}\\{{q}^{\mathrm{2}} =\frac{{p}^{\mathrm{3}} −\mathrm{15}}{{p}}}\end{cases} \\ $$$${p}^{\mathrm{2}} +\mathrm{2}{p}−\mathrm{11}=\frac{{p}^{\mathrm{3}} −\mathrm{15}}{{p}} \\ $$$${p}^{\mathrm{2}} −\frac{\mathrm{11}}{\mathrm{2}}{p}+\frac{\mathrm{15}}{\mathrm{2}}=\mathrm{0} \\ $$$${p}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{2}}\wedge{p}_{\mathrm{2}} =\mathrm{3} \\ $$$$\Rightarrow \\ $$$${q}_{\mathrm{1}} =\pm\frac{\mathrm{1}}{\mathrm{2}}\wedge{q}_{\mathrm{2}} =\pm\mathrm{2} \\ $$$$\Rightarrow \\ $$$$\left({x}=\mathrm{2}\wedge{y}=\mathrm{3}\right)\vee\left({x}=\mathrm{3}\wedge{y}=\mathrm{2}\right)\vee \\ $$$$\:\:\:\:\:\left({x}=\mathrm{1}\wedge{y}=\mathrm{5}\right)\vee\left({x}=\mathrm{5}\wedge{y}=\mathrm{1}\right) \\ $$
Answered by behi83417@gmail.com last updated on 26/May/20
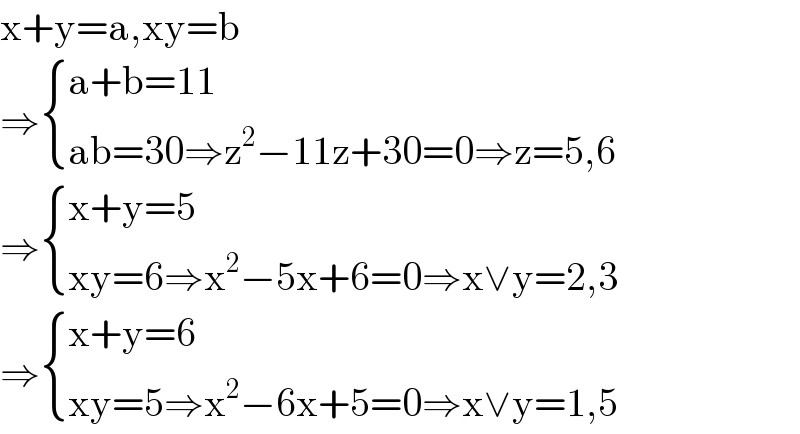
$$\mathrm{x}+\mathrm{y}=\mathrm{a},\mathrm{xy}=\mathrm{b} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{11}}\\{\mathrm{ab}=\mathrm{30}\Rightarrow\mathrm{z}^{\mathrm{2}} −\mathrm{11z}+\mathrm{30}=\mathrm{0}\Rightarrow\mathrm{z}=\mathrm{5},\mathrm{6}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{xy}=\mathrm{6}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{x}\vee\mathrm{y}=\mathrm{2},\mathrm{3}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{6}}\\{\mathrm{xy}=\mathrm{5}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{5}=\mathrm{0}\Rightarrow\mathrm{x}\vee\mathrm{y}=\mathrm{1},\mathrm{5}}\end{cases} \\ $$
