Question Number 95697 by i jagooll last updated on 27/May/20
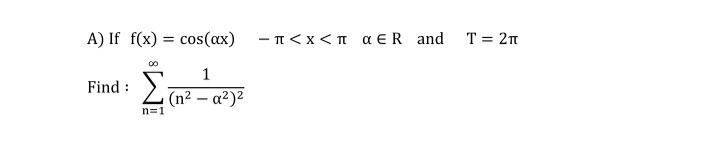
Answered by john santu last updated on 27/May/20
![a_0 = (1/(2π)) ∫_(−π) ^π cos at dt = (1/(2πa)) [sin at ]_(−π) ^π = ((sin πa)/(aπ)) . a_n = (1/(2π)) ∫_(−π) ^π cos (a+n)t +cos (a−n)t dt a_n = ((2a(−1)^n sin aπ)/(π(a^2 −n^2 ))) . ; b_n = 0 ⇒(1/π)∫_(−π) ^π cos^2 at dt = 2a_0 + Σ_(n = 1) ^∞ (a_n ^2 +b_n ^2 ) ⇒1+((sin 2πa)/(2a)) = 2(((sin πa)/(aπ)))^2 +Σ_(n = 1) ^∞ ((4a^2 sin^2 aπ)/(π^2 (n^2 −a^2 )^2 )) ⇒Σ_(n = 1) ^∞ (1/((n^2 −a^2 )^2 )) = (π^2 /(4a^2 sin^2 aπ)) [1+((sin 2πa)/(2a))] −(1/(2a^4 ))](https://www.tinkutara.com/question/Q95719.png)
$${a}_{\mathrm{0}} =\:\frac{\mathrm{1}}{\mathrm{2}\pi}\:\underset{−\pi} {\overset{\pi} {\int}}\:\mathrm{cos}\:{at}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}\pi{a}}\:\left[\mathrm{sin}\:{at}\:\right]_{−\pi} ^{\pi} \\ $$$$=\:\frac{\mathrm{sin}\:\pi{a}}{{a}\pi}\:. \\ $$$${a}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}\pi}\:\underset{−\pi} {\overset{\pi} {\int}}\:\mathrm{cos}\:\left({a}+{n}\right){t}\:+\mathrm{cos}\:\left({a}−{n}\right){t}\:{dt} \\ $$$${a}_{{n}} \:=\:\frac{\mathrm{2}{a}\left(−\mathrm{1}\right)^{{n}} \:\mathrm{sin}\:{a}\pi}{\pi\left({a}^{\mathrm{2}} −{n}^{\mathrm{2}} \right)}\:.\:;\:{b}_{{n}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\pi}\underset{−\pi} {\overset{\pi} {\int}}\:\mathrm{cos}\:^{\mathrm{2}} {at}\:{dt}\:=\:\mathrm{2}{a}_{\mathrm{0}} \:+\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\left({a}_{{n}} ^{\mathrm{2}} +{b}_{{n}} ^{\mathrm{2}} \right)\: \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{2}\pi{a}}{\mathrm{2}{a}}\:=\:\mathrm{2}\left(\frac{\mathrm{sin}\:\pi{a}}{{a}\pi}\right)^{\mathrm{2}} +\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {a}\pi}{\pi^{\mathrm{2}} \left(\mathrm{n}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {a}\pi}\:\left[\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{2}\pi{a}}{\mathrm{2}{a}}\right]\:−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{4}} }\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 27/May/20
![let developp f at fourier serie f(x) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) f(x)cos(nx)dx =(1/π)∫_(−π) ^π cos(αx)cos(nx)dx =(2/π) ∫_0 ^π cos(αx)cos(nx)dx ⇒(π/2)a_n =(1/2)∫_0 ^π (cos(n+α)x +cos(n−α)x)dx ⇒πa_n =[(1/(n+α)) sin(n+α)x +(1/(n−α)) sin(n−α)x]_0 ^π =(1/(n+α))sin(nπ +απ)+(1/(n−α))sin(nπ−απ) =(((−1)^n sin(απ))/(n+α)) +((−(−1)^n sin(απ))/(n−α)) =(−1)^n sin(απ){(1/(n+α))−(1/(n−α))} =(−1)^n sin(απ)(((−2α)/(n^2 −α^2 ))) a_0 =(2/π)∫_0 ^π cos(αx)dx =(2/π)((1/α)sin(απ)) ⇒(a_0 /2) =((sin(πα))/(πα)) ⇒ cos(αx) =((sin(πα))/(πα)) −((2α)/π)Σ_(n=1) ^∞ (((−1)^n sin(απ))/(n^2 −α^2 )) cos(nx) ⇒ ((cos(αx))/(sin(πα))) =(1/(πα)) −((2α)/π) Σ_(n=1) ^∞ (((−1)^n cos(nx))/(n^2 −α^2 )) x=π ⇒cota(πα) =(1/(πα))−((2α)/π) Σ_(n=1) ^∞ (1/((n^2 −α^2 ))) ⇒ cotan(πα)−(1/(πα)) =−((2α)/π) Σ_(n=1) ^∞ (1/(n^2 −α^2 )) ⇒ ((cotan(πα))/α)−(1/(πα^2 )) =−(2/π) Σ_(n=1) ^∞ (1/(n^2 −α^2 )) ⇒ (d/dα)( ((cotan(πα))/α)−(1/(πα^2 ))) =(2/π) Σ_(n=1) ^∞ ((−2α)/((n^2 −α^2 )^2 )) =((−4α)/π) Σ_(n=1) ^∞ (1/((n^2 −α^2 )^2 )) ⇒ Σ_(n=1) ^∞ (1/((n^2 −α^2 )^2 )) =−(π/(4α))×(d/dα)(((cotan(πα))/α)−(1/(πα^2 ))) rest to finish the calculus](https://www.tinkutara.com/question/Q95757.png)
$$\mathrm{let}\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie}\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{T}}\int_{\left[\mathrm{T}\right]} \:\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\pi}\int_{−\pi} ^{\pi} \:\mathrm{cos}\left(\alpha\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\alpha\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:\Rightarrow\frac{\pi}{\mathrm{2}}\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \:\:\left(\mathrm{cos}\left(\mathrm{n}+\alpha\right)\mathrm{x}\:+\mathrm{cos}\left(\mathrm{n}−\alpha\right)\mathrm{x}\right)\mathrm{dx} \\ $$$$\Rightarrow\pi\mathrm{a}_{\mathrm{n}} =\left[\frac{\mathrm{1}}{\mathrm{n}+\alpha}\:\mathrm{sin}\left(\mathrm{n}+\alpha\right)\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{n}−\alpha}\:\mathrm{sin}\left(\mathrm{n}−\alpha\right)\mathrm{x}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\alpha}\mathrm{sin}\left(\mathrm{n}\pi\:+\alpha\pi\right)+\frac{\mathrm{1}}{\mathrm{n}−\alpha}\mathrm{sin}\left(\mathrm{n}\pi−\alpha\pi\right) \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\alpha\pi\right)}{\mathrm{n}+\alpha}\:+\frac{−\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\alpha\pi\right)}{\mathrm{n}−\alpha}\:=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\alpha\pi\right)\left\{\frac{\mathrm{1}}{\mathrm{n}+\alpha}−\frac{\mathrm{1}}{\mathrm{n}−\alpha}\right\} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\alpha\pi\right)\left(\frac{−\mathrm{2}\alpha}{\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} }\right) \\ $$$$\mathrm{a}_{\mathrm{0}} =\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\alpha\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{2}}{\pi}\left(\frac{\mathrm{1}}{\alpha}\mathrm{sin}\left(\alpha\pi\right)\right)\:\Rightarrow\frac{\mathrm{a}_{\mathrm{0}} }{\mathrm{2}}\:=\frac{\mathrm{sin}\left(\pi\alpha\right)}{\pi\alpha}\:\Rightarrow \\ $$$$\mathrm{cos}\left(\alpha\mathrm{x}\right)\:=\frac{\mathrm{sin}\left(\pi\alpha\right)}{\pi\alpha}\:−\frac{\mathrm{2}\alpha}{\pi}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\alpha\pi\right)}{\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} }\:\mathrm{cos}\left(\mathrm{nx}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{cos}\left(\alpha\mathrm{x}\right)}{\mathrm{sin}\left(\pi\alpha\right)}\:=\frac{\mathrm{1}}{\pi\alpha}\:−\frac{\mathrm{2}\alpha}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} } \\ $$$$\mathrm{x}=\pi\:\Rightarrow\mathrm{cota}\left(\pi\alpha\right)\:=\frac{\mathrm{1}}{\pi\alpha}−\frac{\mathrm{2}\alpha}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\mathrm{cotan}\left(\pi\alpha\right)−\frac{\mathrm{1}}{\pi\alpha}\:=−\frac{\mathrm{2}\alpha}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{cotan}\left(\pi\alpha\right)}{\alpha}−\frac{\mathrm{1}}{\pi\alpha^{\mathrm{2}} }\:=−\frac{\mathrm{2}}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(\:\frac{\mathrm{cotan}\left(\pi\alpha\right)}{\alpha}−\frac{\mathrm{1}}{\pi\alpha^{\mathrm{2}} }\right)\:=\frac{\mathrm{2}}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{−\mathrm{2}\alpha}{\left(\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{−\mathrm{4}\alpha}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)^{\mathrm{2}} }\:=−\frac{\pi}{\mathrm{4}\alpha}×\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(\frac{\mathrm{cotan}\left(\pi\alpha\right)}{\alpha}−\frac{\mathrm{1}}{\pi\alpha^{\mathrm{2}} }\right)\:\mathrm{rest}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{the}\:\mathrm{calculus} \\ $$
