Menu Close

Question-95707

Tinku Tara 0 Comments
Pin




Question Number 95707 by john santu last updated on 27/May/20
Commented by john santu last updated on 27/May/20
find the shaded area
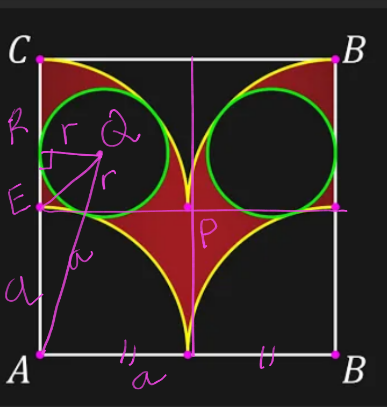
$$\mathrm{find}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{area}\: \\ $$
Commented by john santu last updated on 27/May/20
Commented by john santu last updated on 27/May/20
RE = (√((a−r)^2 −r^2 )) = (√(a^2 −2ar)) AQ^2 = r^2 +AR^2 a^2 +2ar+r^2 =r^2 +(a+(√(a^2 −2ar)))^2 a^2 +2ar=a^2 +2a(√(a^2 −2ar))+a^2 −2ar 4ar=a^2 +2a(√(a^2 −2ar)) 4r −a = 2(√(a^2 −2ar)) 16r^2 −8ar+a^2 =4a^2 −8ar r^2 = (3/(16))a^2 . area 2 small circle =2πr^2 = 2π ((3/(16))a^2 )=((3π)/8)a^2 shaded area = 2a×a−((3πa^2 )/8) = 2a^2 −((3πa^2 )/8)= (((16−3π)/8))a^2
$$\mathrm{RE}\:=\:\sqrt{\left(\mathrm{a}−\mathrm{r}\right)^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2ar}} \\ $$$$\mathrm{AQ}^{\mathrm{2}} \:=\:\mathrm{r}^{\mathrm{2}} +\mathrm{AR}^{\mathrm{2}} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{2ar}+\mathrm{r}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} +\left(\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2ar}}\right)^{\mathrm{2}} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{2ar}=\mathrm{a}^{\mathrm{2}} +\mathrm{2a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2ar}}+\mathrm{a}^{\mathrm{2}} −\mathrm{2ar} \\ $$$$\mathrm{4ar}=\mathrm{a}^{\mathrm{2}} +\mathrm{2a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2ar}} \\ $$$$\mathrm{4r}\:−\mathrm{a}\:=\:\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2ar}}\: \\ $$$$\mathrm{16r}^{\mathrm{2}} −\mathrm{8ar}+\mathrm{a}^{\mathrm{2}} =\mathrm{4a}^{\mathrm{2}} −\mathrm{8ar} \\ $$$$\mathrm{r}^{\mathrm{2}} =\:\frac{\mathrm{3}}{\mathrm{16}}\mathrm{a}^{\mathrm{2}} \:.\:\mathrm{area}\:\mathrm{2}\:\mathrm{small}\:\mathrm{circle} \\ $$$$=\mathrm{2}\pi\mathrm{r}^{\mathrm{2}} \:=\:\mathrm{2}\pi\:\left(\frac{\mathrm{3}}{\mathrm{16}}\mathrm{a}^{\mathrm{2}} \right)=\frac{\mathrm{3}\pi}{\mathrm{8}}\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{shaded}\:\mathrm{area}\:=\:\mathrm{2a}×\mathrm{a}−\frac{\mathrm{3}\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=\:\mathrm{2a}^{\mathrm{2}} −\frac{\mathrm{3}\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{8}}=\:\left(\frac{\mathrm{16}−\mathrm{3}\pi}{\mathrm{8}}\right)\mathrm{a}^{\mathrm{2}} \: \\ $$
Answered by mr W last updated on 27/May/20
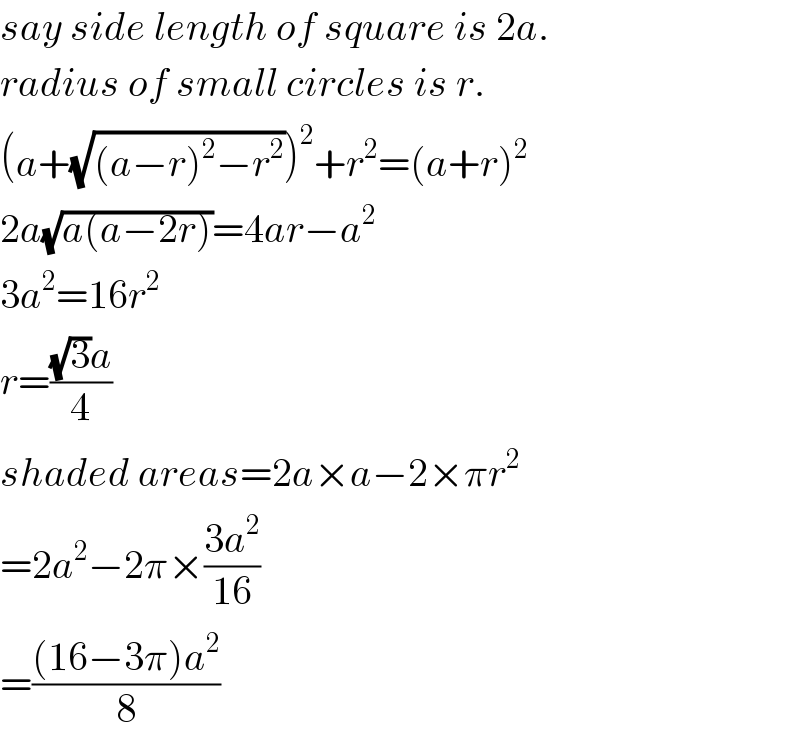
say side length of square is 2a. radius of small circles is r. (a+(√((a−r)^2 −r^2 )))^2 +r^2 =(a+r)^2 2a(√(a(a−2r)))=4ar−a^2 3a^2 =16r^2 r=(((√3)a)/4) shaded areas=2a×a−2×πr^2 =2a^2 −2π×((3a^2 )/(16)) =(((16−3π)a^2 )/8)
$${say}\:{side}\:{length}\:{of}\:{square}\:{is}\:\mathrm{2}{a}. \\ $$$${radius}\:{of}\:{small}\:{circles}\:{is}\:{r}. \\ $$$$\left({a}+\sqrt{\left({a}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)^{\mathrm{2}} +{r}^{\mathrm{2}} =\left({a}+{r}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{a}\sqrt{{a}\left({a}−\mathrm{2}{r}\right)}=\mathrm{4}{ar}−{a}^{\mathrm{2}} \\ $$$$\mathrm{3}{a}^{\mathrm{2}} =\mathrm{16}{r}^{\mathrm{2}} \\ $$$${r}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{4}} \\ $$$${shaded}\:{areas}=\mathrm{2}{a}×{a}−\mathrm{2}×\pi{r}^{\mathrm{2}} \\ $$$$=\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}\pi×\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{16}} \\ $$$$=\frac{\left(\mathrm{16}−\mathrm{3}\pi\right){a}^{\mathrm{2}} }{\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *