Menu Close

Question-95767

Tinku Tara 0 Comments
Pin




Question Number 95767 by PengagumRahasiamu last updated on 27/May/20
Answered by prakash jain last updated on 27/May/20
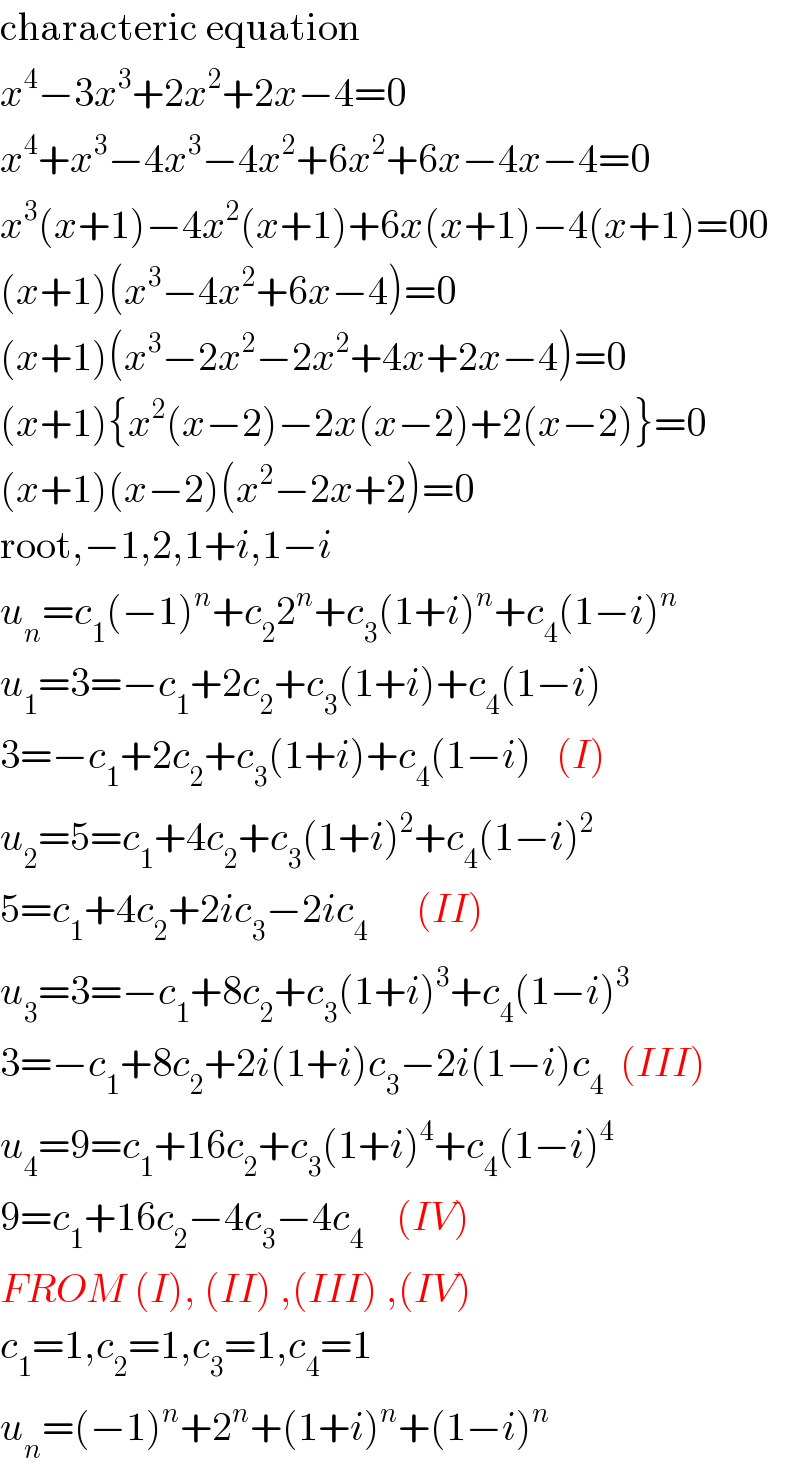
characteric equation x^4 −3x^3 +2x^2 +2x−4=0 x^4 +x^3 −4x^3 −4x^2 +6x^2 +6x−4x−4=0 x^3 (x+1)−4x^2 (x+1)+6x(x+1)−4(x+1)=00 (x+1)(x^3 −4x^2 +6x−4)=0 (x+1)(x^3 −2x^2 −2x^2 +4x+2x−4)=0 (x+1){x^2 (x−2)−2x(x−2)+2(x−2)}=0 (x+1)(x−2)(x^2 −2x+2)=0 root,−1,2,1+i,1−i u_n =c_1 (−1)^n +c_2 2^n +c_3 (1+i)^n +c_4 (1−i)^n u_1 =3=−c_1 +2c_2 +c_3 (1+i)+c_4 (1−i) 3=−c_1 +2c_2 +c_3 (1+i)+c_4 (1−i) (I) u_2 =5=c_1 +4c_2 +c_3 (1+i)^2 +c_4 (1−i)^2 5=c_1 +4c_2 +2ic_3 −2ic_4 (II) u_3 =3=−c_1 +8c_2 +c_3 (1+i)^3 +c_4 (1−i)^3 3=−c_1 +8c_2 +2i(1+i)c_3 −2i(1−i)c_4 (III) u_4 =9=c_1 +16c_2 +c_3 (1+i)^4 +c_4 (1−i)^4 9=c_1 +16c_2 −4c_3 −4c_4 (IV) FROM (I), (II) ,(III) ,(IV) c_1 =1,c_2 =1,c_3 =1,c_4 =1 u_n =(−1)^n +2^n +(1+i)^n +(1−i)^n
$$\mathrm{characteric}\:\mathrm{equation} \\ $$$${x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{4}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{4}{x}−\mathrm{4}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)−\mathrm{4}{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\mathrm{6}{x}\left({x}+\mathrm{1}\right)−\mathrm{4}\left({x}+\mathrm{1}\right)=\mathrm{00} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left\{{x}^{\mathrm{2}} \left({x}−\mathrm{2}\right)−\mathrm{2}{x}\left({x}−\mathrm{2}\right)+\mathrm{2}\left({x}−\mathrm{2}\right)\right\}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{root},−\mathrm{1},\mathrm{2},\mathrm{1}+{i},\mathrm{1}−{i} \\ $$$${u}_{{n}} ={c}_{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} +{c}_{\mathrm{2}} \mathrm{2}^{{n}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)^{{n}} +{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right)^{{n}} \\ $$$${u}_{\mathrm{1}} =\mathrm{3}=−{c}_{\mathrm{1}} +\mathrm{2}{c}_{\mathrm{2}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)+{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right) \\ $$$$\mathrm{3}=−{c}_{\mathrm{1}} +\mathrm{2}{c}_{\mathrm{2}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)+{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right)\:\:\:\left({I}\right) \\ $$$${u}_{\mathrm{2}} =\mathrm{5}={c}_{\mathrm{1}} +\mathrm{4}{c}_{\mathrm{2}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)^{\mathrm{2}} +{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right)^{\mathrm{2}} \\ $$$$\mathrm{5}={c}_{\mathrm{1}} +\mathrm{4}{c}_{\mathrm{2}} +\mathrm{2}{ic}_{\mathrm{3}} −\mathrm{2}{ic}_{\mathrm{4}} \:\:\:\:\:\:\left({II}\right) \\ $$$${u}_{\mathrm{3}} =\mathrm{3}=−{c}_{\mathrm{1}} +\mathrm{8}{c}_{\mathrm{2}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)^{\mathrm{3}} +{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right)^{\mathrm{3}} \\ $$$$\mathrm{3}=−{c}_{\mathrm{1}} +\mathrm{8}{c}_{\mathrm{2}} +\mathrm{2}{i}\left(\mathrm{1}+{i}\right){c}_{\mathrm{3}} −\mathrm{2}{i}\left(\mathrm{1}−{i}\right){c}_{\mathrm{4}} \:\:\left({III}\right) \\ $$$${u}_{\mathrm{4}} =\mathrm{9}={c}_{\mathrm{1}} +\mathrm{16}{c}_{\mathrm{2}} +{c}_{\mathrm{3}} \left(\mathrm{1}+{i}\right)^{\mathrm{4}} +{c}_{\mathrm{4}} \left(\mathrm{1}−{i}\right)^{\mathrm{4}} \\ $$$$\mathrm{9}={c}_{\mathrm{1}} +\mathrm{16}{c}_{\mathrm{2}} −\mathrm{4}{c}_{\mathrm{3}} −\mathrm{4}{c}_{\mathrm{4}} \:\:\:\:\left({IV}\right) \\ $$$${FROM}\:\left({I}\right),\:\left({II}\right)\:,\left({III}\right)\:,\left({IV}\right) \\ $$$${c}_{\mathrm{1}} =\mathrm{1},{c}_{\mathrm{2}} =\mathrm{1},{c}_{\mathrm{3}} =\mathrm{1},{c}_{\mathrm{4}} =\mathrm{1} \\ $$$${u}_{{n}} =\left(−\mathrm{1}\right)^{{n}} +\mathrm{2}^{{n}} +\left(\mathrm{1}+{i}\right)^{{n}} +\left(\mathrm{1}−{i}\right)^{{n}} \\ $$
Commented by bobhans last updated on 27/May/20
great
$$\mathrm{great} \\ $$
Commented by PengagumRahasiamu last updated on 21/Jul/20
Thank you Sir

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *