Question Number 95773 by Fikret last updated on 27/May/20
Answered by Fikret last updated on 27/May/20

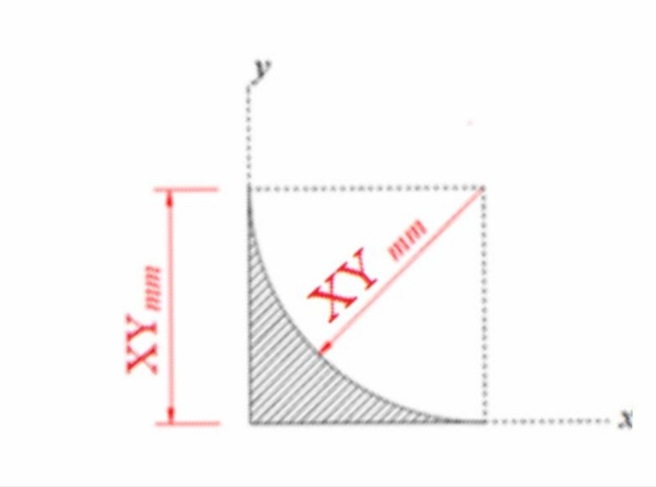
$$ \\ $$$${find}\:{the}\:{geometrical}\:{centers}\:{of}\: \\ $$$${the}\:{following}\:{sections} \\ $$
Answered by john santu last updated on 27/May/20
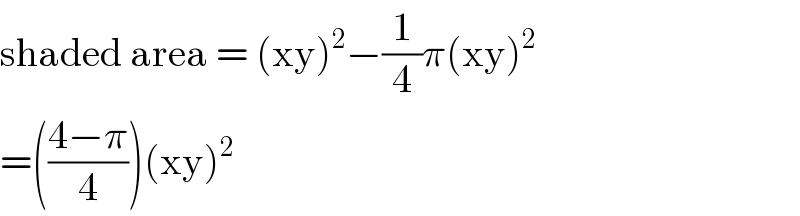
$$\mathrm{shaded}\:\mathrm{area}\:=\:\left(\mathrm{xy}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\left(\mathrm{xy}\right)^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{4}−\pi}{\mathrm{4}}\right)\left(\mathrm{xy}\right)^{\mathrm{2}} \\ $$
Commented by Fikret last updated on 27/May/20

$${wanted}\:{geommetrik}\:{center} \\ $$
Answered by mr W last updated on 27/May/20
Commented by mr W last updated on 27/May/20
![a=XY y=(√(a^2 −x^2 )) x_G =((∫_0 ^a (a−(√(a^2 −x^2 )))xdx)/(∫_0 ^a (a−(√(a^2 −x^2 )))dx)) =(((a^3 /2)+(1/3)[(a^2 −x^2 )^(3/2) ]_0 ^a )/(a^2 −(1/2)[a^2 sin^(−1) (x/a)+x(√(a^2 −x^2 ))]_0 ^a )) =(((a^3 /2)−(a^3 /3))/(a^2 −((πa^2 )/4))) =((2a)/(3(4−π))) x_G ^′ =a−x_G =(((10−3π)a)/(3(4−π)))≈0.2234a y_G ^′ =x_G ^′ =(((10−3π)a)/(3(4−π)))≈0.2234a](https://www.tinkutara.com/question/Q95817.png)
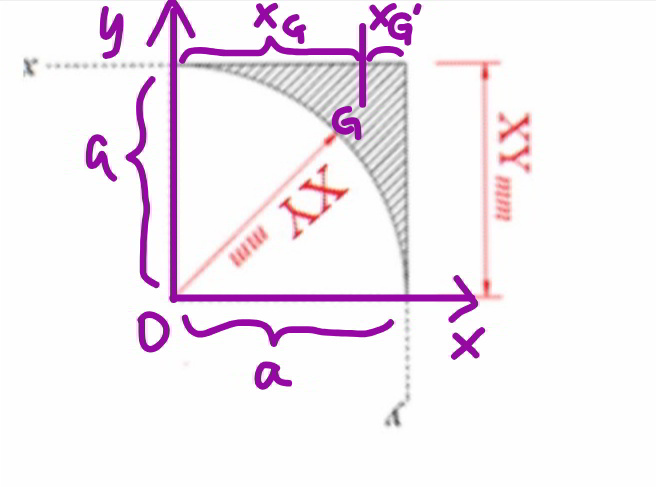
$${a}={XY} \\ $$$${y}=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${x}_{{G}} =\frac{\int_{\mathrm{0}} ^{{a}} \left({a}−\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right){xdx}}{\int_{\mathrm{0}} ^{{a}} \left({a}−\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right){dx}} \\ $$$$=\frac{\frac{{a}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\left[\left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{{a}} }{{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left[{a}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \frac{{x}}{{a}}+{x}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{{a}} } \\ $$$$=\frac{\frac{{a}^{\mathrm{3}} }{\mathrm{2}}−\frac{{a}^{\mathrm{3}} }{\mathrm{3}}}{{a}^{\mathrm{2}} −\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\frac{\mathrm{2}{a}}{\mathrm{3}\left(\mathrm{4}−\pi\right)} \\ $$$${x}_{{G}} ^{'} ={a}−{x}_{{G}} =\frac{\left(\mathrm{10}−\mathrm{3}\pi\right){a}}{\mathrm{3}\left(\mathrm{4}−\pi\right)}\approx\mathrm{0}.\mathrm{2234}{a} \\ $$$${y}_{{G}} ^{'} ={x}_{{G}} ^{'} =\frac{\left(\mathrm{10}−\mathrm{3}\pi\right){a}}{\mathrm{3}\left(\mathrm{4}−\pi\right)}\approx\mathrm{0}.\mathrm{2234}{a} \\ $$
Answered by mr W last updated on 27/May/20
Commented by mr W last updated on 27/May/20
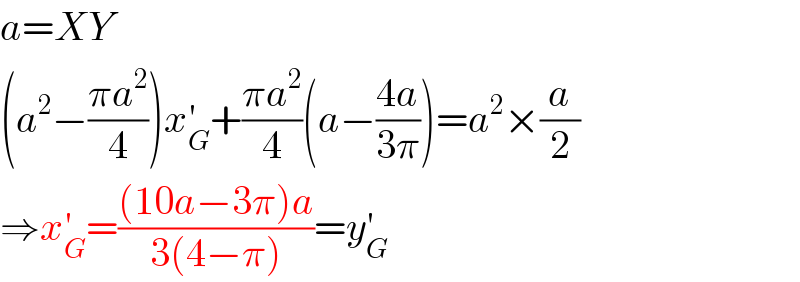
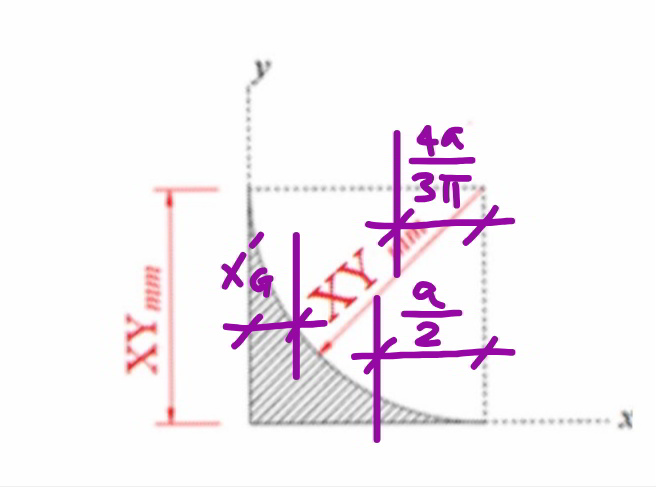
$${a}={XY} \\ $$$$\left({a}^{\mathrm{2}} −\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}\right){x}_{{G}} ^{'} +\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}\left({a}−\frac{\mathrm{4}{a}}{\mathrm{3}\pi}\right)={a}^{\mathrm{2}} ×\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{G}} ^{'} =\frac{\left(\mathrm{10}{a}−\mathrm{3}\pi\right){a}}{\mathrm{3}\left(\mathrm{4}−\pi\right)}={y}_{{G}} ^{'} \\ $$
Commented by mr W last updated on 27/May/20
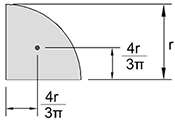
Commented by Fikret last updated on 27/May/20

$${thank}\:{you}\: \\ $$
