Question Number 95830 by I want to learn more last updated on 27/May/20
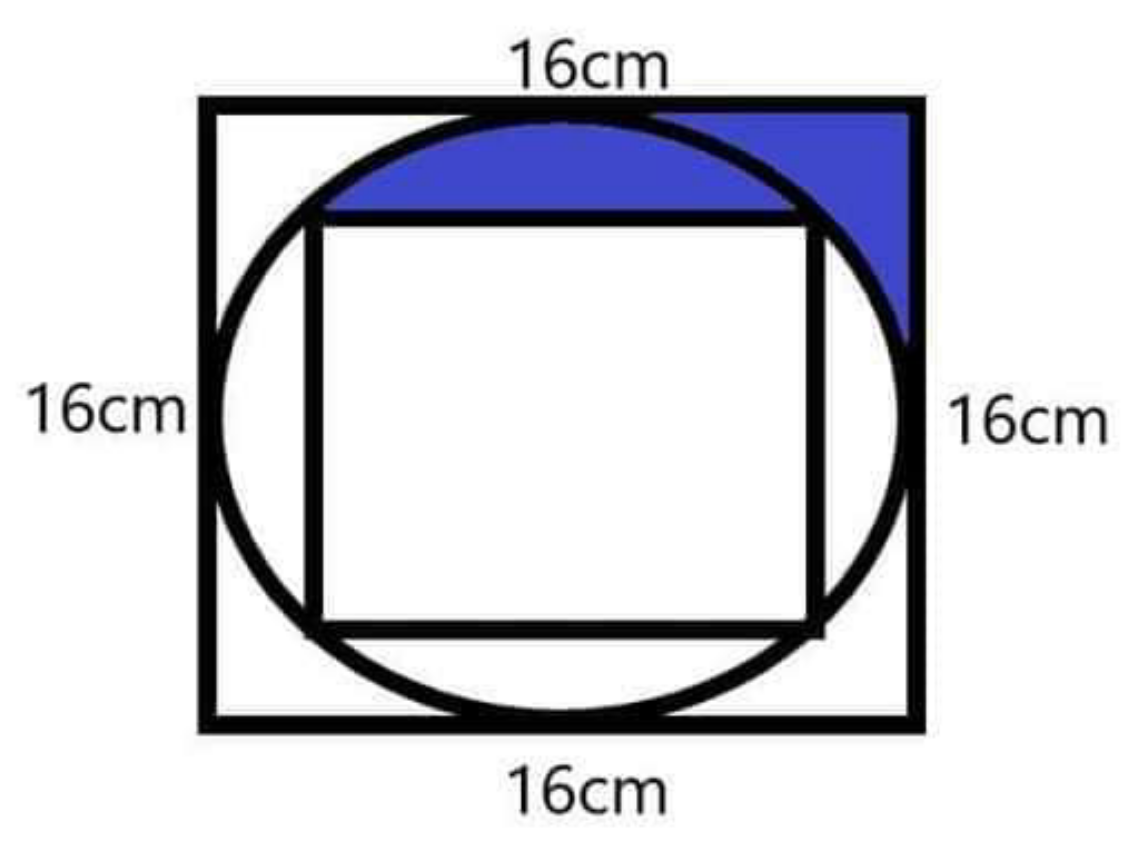
Answered by behi83417@gmail.com last updated on 28/May/20
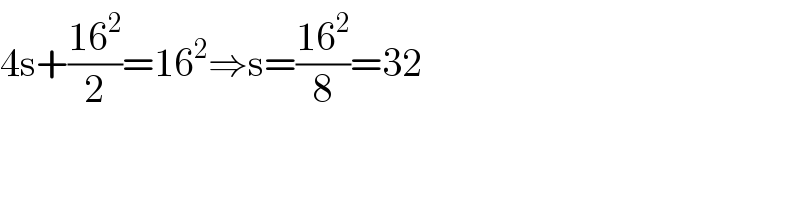
$$\mathrm{4s}+\frac{\mathrm{16}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{16}^{\mathrm{2}} \Rightarrow\mathrm{s}=\frac{\mathrm{16}^{\mathrm{2}} }{\mathrm{8}}=\mathrm{32} \\ $$
Answered by john santu last updated on 28/May/20
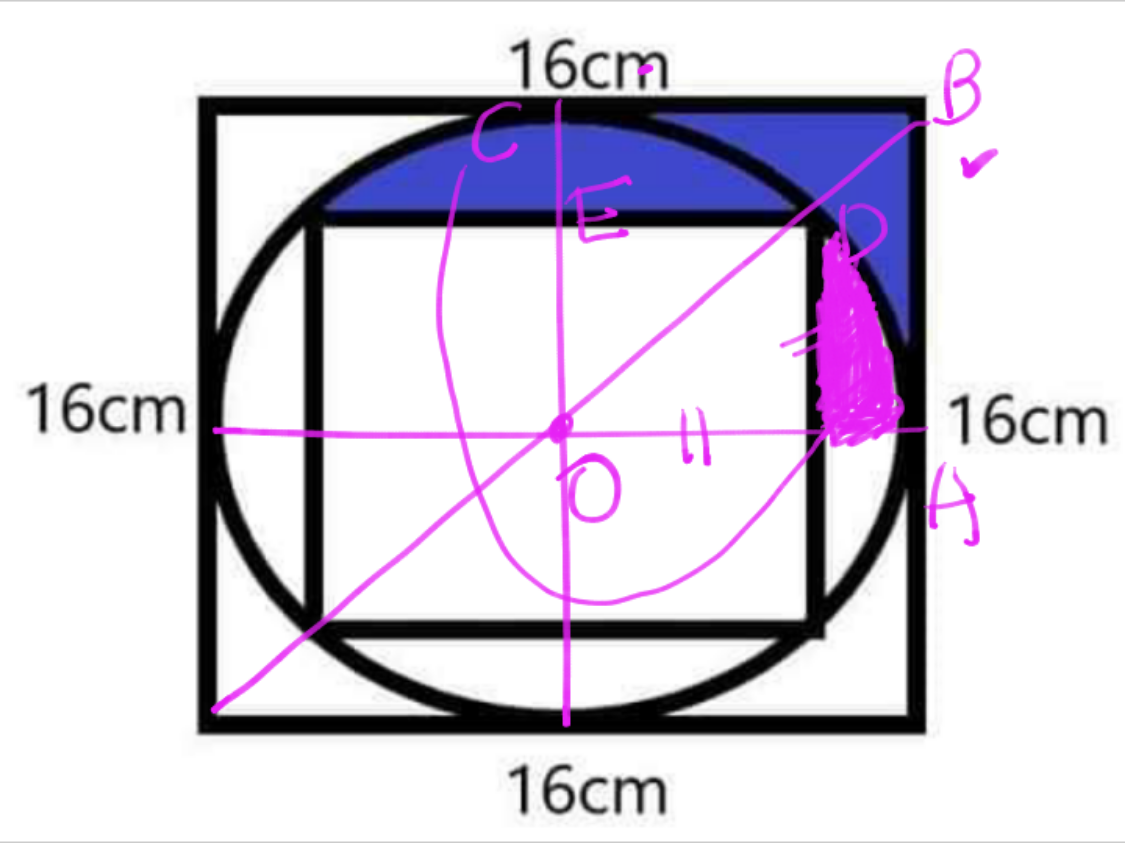
Commented by john santu last updated on 28/May/20

$$\mathrm{shaded}\:\mathrm{area}\:=\:\mathrm{8}^{\mathrm{2}} −\mathrm{area}\:\mathrm{OFDE} \\ $$$$\mathrm{let}\:\mathrm{OF}\:=\:\mathrm{a}\:\Rightarrow\:\mathrm{OD}^{\mathrm{2}} =\mathrm{OF}^{\mathrm{2}} +\mathrm{DF}^{\mathrm{2}} \\ $$$$\mathrm{64}\:=\:\mathrm{2a}^{\mathrm{2}} \:\Rightarrow\:\mathrm{a}^{\mathrm{2}} \:=\:\mathrm{32}\: \\ $$$$\mathrm{then}\:\mathrm{shaded}\:\mathrm{area}\:=\:\mathrm{64}−\mathrm{32}\:=\:\mathrm{32}\: \\ $$
